
分析 (1)利用古典概型的概率公式,利用列举法进行求解即可;
(2)利用几何概型的概率公式,求出对应的面积进行求解即可.
解答 解:(1)设函数f(x)有零点为事件A,m,n都是从集合{1,2,3}中任取的数字,依题意得
所有的基本事件为(1,1),(1,2),(1,3),(2,1),(2,2),(2,3),(3,1),(3,2),(3,3),其中第一个数表示m的取值,第二个数表示n的取值,即基本事件总数为N=9
若函数f(x)=x2-4mx+4n2有零点则△=16m2-16m2≥0,等价于m≥n
事件A所含的基本事件为(1,1),(2,1),(2,2),(3,1),(3,2),(3,3),
则M=6,P(A)=$\frac{6}{9}$=$\frac{2}{3}$
(2)设在区间[0,4]内任取两个实数x,y,“x2+y2>(m-n)2恒成立”为事件C则事件C等价于“x2+y2>9”,(x,y)可以看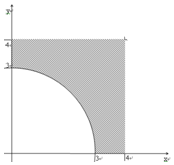 成平面中的点,则全部结果所构成的区域Ω={(x,y)|0≤x≤4,0≤y≤4,x,y∈R},
成平面中的点,则全部结果所构成的区域Ω={(x,y)|0≤x≤4,0≤y≤4,x,y∈R},
而事件B所构成的区域B={(x,y)|x2+y2>9,(x,y)∈Ω}.如图所示(阴影部分表示事件C)
SΩ=4×4=16,SC=16-$\frac{9π}{4}$,
∴P(C)=$\frac{16-\frac{9π}{4}}{16}$=1-$\frac{9}{64}$π
点评 本题主要考查古典概型和几何概型概率的计算,利用列举法以及转化法是解决本题的关键.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{6}$ | B. | $\frac{1}{10}$ | C. | $\frac{1}{2}$ | D. | $\frac{5}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,2) | B. | (0,1) | C. | (-2,2) | D. | (-∞,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3\sqrt{2}}{2}$ | B. | $\sqrt{14}$ | C. | $\frac{\sqrt{14}}{2}$ | D. | $\frac{7}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com