
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
分析 ①由偶函数的定义进行判断.
②由周期函数的定义证明
③由解析式做出大致图象:根据图象进行判断即可.
解答 解:函数f(x)=$\left\{\begin{array}{l}{1,x为有理数}\\{0,x为无理数}\end{array}\right.$,
对于①,定义域为R,x为有理数,-x为有理数,
f(-x)=1=f(x);
x为无理数,-x为无理数,
f(-x)=0=f(x),
则f(-x)=f(x),x∈R,
则f(x)为偶函数;
对于②,存在非零有理数T,
当x为有理数时,x+T为有理数,
f(x+T)=1=f(x);
当x为无理数时,x+T为无理数,
f(x+T)=0=f(x);
则f(x)为周期函数;
对于③,设三个点(x1,0)(x2,1)(x3,0),
且x1+x3=2x2,x3-x2=$\frac{\sqrt{3}}{3}$,比如x1=1-$\frac{\sqrt{3}}{3}$,x2=1,x3=1+$\frac{\sqrt{3}}{3}$.
易满足三点构成三角形是等边三角形,故③正确.
故正确的个数为3.
故选:D.
点评 本题主要考查了特殊函数的性质的理解和运用,考查函数的奇偶性和周期性,属于中档题.


 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:高中数学 来源: 题型:选择题
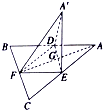 如图,边长为a的等边三角形ABC的中线AF与中位线DE交于点G,已知△A'DE是△ADE绕DE旋转过程中的一个图形,则下列命题中正确的是( )
如图,边长为a的等边三角形ABC的中线AF与中位线DE交于点G,已知△A'DE是△ADE绕DE旋转过程中的一个图形,则下列命题中正确的是( )| A. | ① | B. | ①② | C. | ①②③ | D. | ②③ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,已知四边形ABDC是圆O的内接四边形,B,D是圆O上的动点,AD与BC交于F,圆O的切线CE(C为切点)与线段AB的延长线交于E,∠BCD=∠CBD.
如图,已知四边形ABDC是圆O的内接四边形,B,D是圆O上的动点,AD与BC交于F,圆O的切线CE(C为切点)与线段AB的延长线交于E,∠BCD=∠CBD.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com