
【题目】若动点![]() 在直线
在直线![]() 上,动点
上,动点![]() 在直线
在直线![]() 上,设线段
上,设线段![]() 的中点为
的中点为![]() ,且
,且![]() ,则
,则![]() 的取值范围是__________.
的取值范围是__________.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和为Sn , 且满足Sn=2an﹣2.若数列{bn}满足bn=10﹣log2an , 则是数列{bn}的前n项和取最大值时n的值为( )
A.8
B.10
C.8或9
D.9或10
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某食品店为了了解气温对销售量的影响,随机记录了该店1月份中5天的日销售量![]() (单位:千克)与该地当日最低气温
(单位:千克)与该地当日最低气温![]() (单位:
(单位: ![]() )的数据,如下表:
)的数据,如下表:
x | 2 | 5 | 8 | 9 | 11 |
y | 12 | 10 | 8 | 8 | 7 |
(1)求出![]() 与
与![]() 的回归方程
的回归方程![]() ;
;
(2)判断![]() 与
与![]() 之间是正相关还是负相关;若该地1月份某天的最低气温为
之间是正相关还是负相关;若该地1月份某天的最低气温为![]() ,请用所求回归方程预测该店当日的销售量;
,请用所求回归方程预测该店当日的销售量;
(3)设该地1月份的日最低气温![]() ~
~![]() ,其中
,其中![]() 近似为样本平均数
近似为样本平均数![]() ,
, ![]() 近似为样本方差
近似为样本方差![]() ,求
,求![]() .
.
附:①回归方程![]() 中,
中, 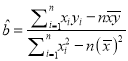 ,
, ![]() .
.
②![]() ,
, ![]() ,若
,若![]() ~
~![]() ,则
,则![]() ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 和定点
和定点![]() ,由圆
,由圆![]() 外一点
外一点![]() 向圆
向圆![]() 引切线
引切线![]() ,切点为
,切点为![]() ,且满足
,且满足![]() .
.
(1)求实数![]() ,
,![]() 满足的等量关系;
满足的等量关系;
(2)求线段![]() 长的最小值;
长的最小值;
(3)若以![]() 为圆心所作的圆
为圆心所作的圆![]() 与圆
与圆![]() 有公共点,试求半径取最小值时圆
有公共点,试求半径取最小值时圆![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,点A(0,3),直线l:y=2x﹣4.设圆C的半径为1,圆心在l上.
(1)若圆心C也在直线y=﹣x+5上,求圆C的方程;
(2)在(1)的条件下,过点A作圆C的切线,求切线的方程;
(3)若圆C上存在点M,使|MA|=|MO|,求圆心C的横坐标a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“累积净化量![]() ”是空气净化器质量的一个重要衡量指标,它是指空气净化从开始使用到净化效率为50%时对颗粒物的累积净化量,以克表示,根据
”是空气净化器质量的一个重要衡量指标,它是指空气净化从开始使用到净化效率为50%时对颗粒物的累积净化量,以克表示,根据![]() 《空气净化器》国家标准,对空气净化器的累计净化量
《空气净化器》国家标准,对空气净化器的累计净化量![]() 有如下等级划分:
有如下等级划分:
累积净化量(克) |
|
|
| 12以上 |
等级 |
|
|
|
|
为了了解一批空气净化器(共5000台)的质量,随机抽取![]() 台机器作为样本进行估计,已知这
台机器作为样本进行估计,已知这![]() 台机器的累积净化量都分布在区间
台机器的累积净化量都分布在区间![]() 中,按照
中,按照![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 均匀分组,其中累积净化量在
均匀分组,其中累积净化量在![]() 的所有数据有:4.5,4.6,5.2,5.3,5.7和5.9,并绘制了频率分布直方图,如图所示:
的所有数据有:4.5,4.6,5.2,5.3,5.7和5.9,并绘制了频率分布直方图,如图所示:
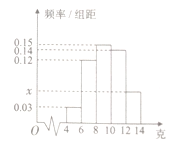
(1)求![]() 的值及频率分布直方图中
的值及频率分布直方图中![]() 的值;
的值;
(2)以样本估计总体,试估计这批空气净化器(共5000台)中等级为![]() 的空气净化器有多少台?
的空气净化器有多少台?
(3)从累积净化量在![]() 的样本中随机抽取2台,求恰好有1台等级为
的样本中随机抽取2台,求恰好有1台等级为![]() 的概率.
的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com