
已知矩阵M=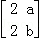 的两个特征值分别为λ1=﹣1和λ2=4.
的两个特征值分别为λ1=﹣1和λ2=4.
(1)求实数a,b的值;
(2)求直线x﹣2y﹣3=0在矩阵M所对应的线性变换作用下的象的方程.
(1)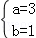 ;(2)5x﹣7y+12=0.
;(2)5x﹣7y+12=0.
【解析】
试题分析:(1)先写出矩阵A的特征多项式,再结合由于λ1=﹣1和λ2=4是此函数的零点即可求得a,b.
(2)先直线x﹣2y﹣3=0上任一点(x,y)在矩阵M所对应的线性变换作用下的像(x′,y′),根据矩阵变换得出它们之间的关系,从而求直线x﹣2y﹣3=0在矩阵M所对应的线性变换作用下的像的方程.
【解析】
(1)矩阵A的特征多项式为:f(λ)= ,
,
即f(λ)=λ2﹣(b+2)λ+2b﹣2a,
由于λ1=﹣1和λ2=4是此函数的零点,
∴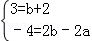 ⇒
⇒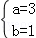
(2)由上知,M=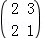 ,
,
设直线x﹣2y﹣3=0上任一点(x,y)
在矩阵M所对应的线性变换作用下的像(x′,y′),
由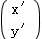 =
=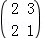
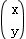 得到:
得到: ,
,
代入x﹣2y﹣3=0化简得到5x′﹣7y′+12=0.
直线x﹣2y﹣3=0在矩阵M所对应的线性变换作用下的像的方程5x﹣7y+12=0.


科目:高中数学 来源:[同步]2014年新人教A版选修4-5 1.2绝对值不等式练习卷(解析版) 题型:选择题
(2014•九江三模)若关于x的不等式|x﹣1|+x≤a无解,则实数a的取值范围是( )
A.(﹣∞,1) B.(﹣∞,1] C.(1,+∞) D.[1,+∞)
查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教A版选修4-5 1.1不等式练习卷(解析版) 题型:选择题
(2014•兴安盟一模)x、y满足约束条件 ,若目标函数z=ax+by(a>0,b>0)的最大值为7,则
,若目标函数z=ax+by(a>0,b>0)的最大值为7,则 的最小值为( )
的最小值为( )
A.14 B.7 C.18 D.13
查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教A版选修4-4 1.4柱坐标系与球坐标系简介(解析版) 题型:填空题
(2008•佛山二模)(坐标系与参数方程)球坐标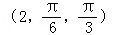 对应的点的直角坐标是 ,对应点的柱坐标是 .
对应的点的直角坐标是 ,对应点的柱坐标是 .
查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教A版选修4-2 4.2特征向量的应用练习卷(解析版) 题型:解答题
(2009•连云港二模)已知二阶矩阵M有特征值λ=8及对应的一个特征向量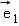 =
=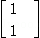 ,并且矩阵M对应的变换将点(﹣1,2)变换成(﹣2,4).
,并且矩阵M对应的变换将点(﹣1,2)变换成(﹣2,4).
(1)求矩阵M;
(2)求矩阵M的另一个特征值,及对应的一个特征向量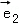 的坐标之间的关系.
的坐标之间的关系.
(3)求直线l:x﹣y+1=0在矩阵M的作用下的直线l′的方程.
查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教A版选修4-2 3.1逆变换与逆矩阵练习卷(解析版) 题型:解答题
(2014•南京三模)已知矩阵A=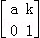 (k≠0)的一个特征向量为α=
(k≠0)的一个特征向量为α=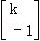 ,A的逆矩阵A﹣1对应的变换将点(3,1)变为点(1,1).求实数a,k的值.
,A的逆矩阵A﹣1对应的变换将点(3,1)变为点(1,1).求实数a,k的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com