
已知二阶矩阵M满足: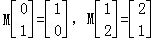 ,求M2.
,求M2.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:[同步]2014年新人教A版选修4-5 1.2绝对值不等式练习卷(解析版) 题型:选择题
(2013•中山模拟)若集合M={x∈N*|x<6},N={x||x﹣1|≤2},则M∩∁RN=( )
A.(﹣∞,﹣1) B.[1,3) C.(3,6) D.{4,5}
查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教A版选修4-4 1.4柱坐标系与球坐标系简介(解析版) 题型:选择题
把点M的直角坐标(﹣1,1,1)化为柱坐标是( )
A.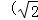 ,
,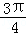 ,1) B.
,1) B.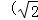 ,
, ,1) C.
,1) C.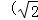 ,
,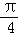 ,1) D.
,1) D.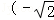 ,
,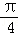 ,1)
,1)
查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教A版选修4-2 4.2特征向量的应用练习卷(解析版) 题型:解答题
已知矩阵M=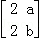 的两个特征值分别为λ1=﹣1和λ2=4.
的两个特征值分别为λ1=﹣1和λ2=4.
(1)求实数a,b的值;
(2)求直线x﹣2y﹣3=0在矩阵M所对应的线性变换作用下的象的方程.
查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教A版选修4-2 4.2特征向量的应用练习卷(解析版) 题型:解答题
设矩阵A= ,矩阵A属于特征值λ1=﹣1的一个特征向量为α1=
,矩阵A属于特征值λ1=﹣1的一个特征向量为α1=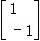 ,属于特征值λ2=4的一个特征向量为α2=
,属于特征值λ2=4的一个特征向量为α2= ,求ad﹣bc的值.
,求ad﹣bc的值.
查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教A版选修4-2 4.2特征向量的应用练习卷(解析版) 题型:填空题
(2009•静安区一模)定义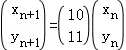 为向量
为向量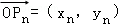 到向量
到向量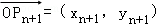 的一个矩阵变换,其中O是坐标原点,n∈N*.已知
的一个矩阵变换,其中O是坐标原点,n∈N*.已知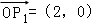 ,则
,则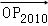 的坐标为 .
的坐标为 .
查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教A版选修4-2 3.3逆矩阵与二元一次方程组(解析版) 题型:填空题
(2014•黄浦区一模)各项都为正数的无穷等比数列{an},满足a2=m,a4=t,且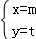 是增广矩阵
是增广矩阵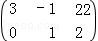 的线性方程组
的线性方程组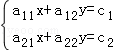 的解,则无穷等比数列{an}各项和的数值是 .
的解,则无穷等比数列{an}各项和的数值是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com