练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    10．将1～9这9个数平均分成3组，则每组的3个数都成等差数列的分组方法的种数是（　　）
    A．3B．5C．7D．9

    分析 利用已知条件列出关系式，列出可能取值，找出等差数列的组数即可．

    解答 解：设3组中每组正中间的数分别a，b，c且a＜b＜c，则3a+3b+3c=45，a+b+c=15，
    而2≤a≤4，故（a，b，c）所有可能取的值为（2，5，8），（2，6，7），（3，4，8），（3，5，7）（4，5，6）此时相对应的分组情况是（1，2，3），（4，5，6），（7，8，9）；（1，2，3），（4，6，8），（5，7，9）；（1，3，5），（2，4，6），（7，8，9）；（2，3，4），（1，5，9），（6，7，8）；（1，4，7），（2，5，8），（3，6，9）故分组方法有5种．
    故选B．

    点评 本题考查等差数列的判断，归纳推理，考查分析问题解决问题的能力．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    20．若复数$\frac{1}{2}$-（a+$\frac{1}{2}$）i（i为虚数单位）在复平面内对应的点在直线x+y=0上，则实数a=（　　）
    A．-1B．0C．1D．2

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    1．设数列{an}的前n项和为Sn，且Sn=2an-1（n=1，2，…）
    （Ⅰ）求数列{an}的通项公式；
    （Ⅱ）若数列{bn}满足bn=$\frac{{2}^{n}}{（{a}_{n}+1）（{a}_{n+1}+1）}$，求数列{bn}的前n项和Tn，并求使Tn$＜\frac{2014}{2015}$成立的n的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    18．用辗转相除法求294和84的最大公约数，则所求最大公约数为 （　　）
    A．21B．42C．84D．168

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    5．在复平面内，复数$\frac{2i}{1-i}$对应的点的坐标是（　　）
    A．（-1，1）B．（-1，-1）C．（1，-1）D．（1，1）

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    15．已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1（a＞b＞0）上任意一点到两焦点F1，F2距离之和为4$\sqrt{2}$，离心率为$\frac{{\sqrt{3}}}{2}$．
    （1）求椭圆的标准方程；
    （2）若直线l的斜率为$\frac{1}{2}$，直线l与椭圆C交于A，B两点．点P（2，1）为椭圆上一点，求△PAB的面积的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    2．设p，q是两个命题，则“p，q均为假命题”是“p∧q为假命题”的（　　）条件．
    A．充分不必要B．必要不充分
    C．充分必要D．既不充分也不必要

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    19．设Sn是等差数列{an}（an≠0）的前n项和，S5=a2+a8，则$\frac{a_5}{a_3}$的值为$\frac{5}{2}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

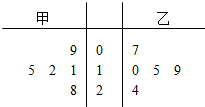    19．某区今年春季运动会共有5场篮球比赛，其中甲、乙两运动员得分的茎叶图如图所示．
    （Ⅰ）求甲、乙两名队员得分的平均值和方差，并判断哪一个队员的成绩更稳定；
    （Ⅱ）在甲队员的得分中任选两个得分，求恰有一个得分不低于平均分的概率．

    查看答案和解析>>

    同步练习册答案