
分析 如果p,q均为真命题,则命题p,q均为真命题,进而可得答案.
解答 解:因为c>0,
若p:函数y=cx在R上递减为真时:0<c<1,
若q:函数f(x)=x2-c2的最小值不大于-$\frac{1}{16}$.为真时:-c2≤-$\frac{1}{16}$,
所以 c≤-$\frac{1}{4}$,或c≥$\frac{1}{4}$,
所以c≥$\frac{1}{4}$; …(6分)
因为p,q均为真命题,所以$\frac{1}{4}$≤c<1,
所以实数c的取值范围为:$\frac{1}{4}$≤c<1 …(10分)
点评 本题以命题的真假判断与应用为载体,考查了指数函数的图象和性质,二次函数的图象和性质,难度基础.


 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案科目:高中数学 来源: 题型:选择题
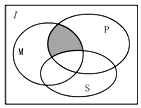
| A. | (M∩P)∪S | B. | (M∩P)∩S | C. | (M∩P)∩(∁IS) | D. | (M∩P)∪(∁IS) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com