
| A. | -8 | B. | 8 | C. | -4 | D. | 4 |
分析 根据条件设x>0,从而有-x<0,这样即可求出f(x)=x(1+x),根据${a}_{1}=\frac{1}{2}$,且${a}_{n+1}=\frac{1}{1-{a}_{n}}$可求数列{an}的前四项,从而会发现该数列是以3为周期的周期数列,这样便可以求出a2015和a2016的值,从而可求出f(a2015)+f(a2016)的值.
解答 解:设x>0,则-x<0;
∵f(x)是定义在R上的奇函数;
∴f(x)=-f(-x)=-[-x(1+x)]=x(1+x);
由${a}_{1}=\frac{1}{2}$,且${a}_{n+1}=\frac{1}{1-{a}_{n}}$得:
${a}_{2}=\frac{1}{1-{a}_{1}}=\frac{1}{1-\frac{1}{2}}=2$,${a}_{3}=\frac{1}{1-{a}_{2}}=\frac{1}{1-2}=-1$,${a}_{4}=\frac{1}{1-{a}_{3}}=\frac{1}{1-(-1)}=\frac{1}{2}$,…;
∴数列{an}是以3为周期的周期数列;
∴a2015=a671×3+2=a2=2,a2016=a671×3+3=a3=-1;
∴f(a2015)+f(a2016)=f(2)+f(-1)=2(1+2)+(-1)(1+1)=4.
故选:D.
点评 考查奇函数的定义,对于奇函数,已知一区间上的解析式,而求其对称区间上的解析式的方法,根据数列的首项和递推公式可以求该数列的前几项,以及周期数列的概念,已知函数求值的方法.


 出彩同步大试卷系列答案
出彩同步大试卷系列答案科目:高中数学 来源: 题型:解答题
 已知p,m>0,抛物线E:x2=2py上一点M(m,2)到抛物线焦点F的距离为$\frac{5}{2}$.
已知p,m>0,抛物线E:x2=2py上一点M(m,2)到抛物线焦点F的距离为$\frac{5}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
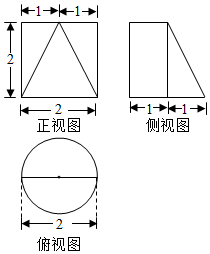
| A. | $\frac{8π}{3}$ | B. | $\frac{4π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [6,7) | B. | (1,2]∪(5,6)∪[7,10) | C. | (1,6) | D. | (1,2]∪(5,6]∪(7,10) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com