
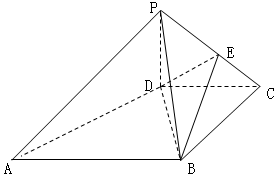
 如图,在四棱锥P-ABCD中,底面ABCD是梯形,AB∥CD,PD⊥平面ABCD,BD⊥DC,PD=BD=DC=$\frac{1}{2}$AB,E为PC中点.
如图,在四棱锥P-ABCD中,底面ABCD是梯形,AB∥CD,PD⊥平面ABCD,BD⊥DC,PD=BD=DC=$\frac{1}{2}$AB,E为PC中点.分析 (I)根据三线合一可得PC⊥DE,PC⊥BE,故而PC⊥平面BDE,于是平面BDE⊥平面PBC;
(II)根据棱锥的体积计算PD,根据VP-ABC=VA-PBC列方程解出A到平面PBC的距离.
解答 证明:(I)PD⊥平面ABCD,CD?平面ABCD,BD?平面ABCD,
∴PD⊥CD,PD⊥DB,又BD⊥DC,
PD=DC=DB,
∴PC=PB=BC,
∵E是PC的中点,
∴PC⊥DE,PC⊥BE,又DE∩BE=E,
∴PC⊥平面BDE,又PC?平面PBC,
∴平面BDE⊥平面PBC.
(Ⅱ)设PD=CD=BD=$\frac{1}{2}AB$=a,
∴S四边形ABCD=$\frac{1}{2}×AB×BD+\frac{1}{2}×CD×BD$=$\frac{3}{2}$a2,
则VP-ABCD=$\frac{1}{3}{S}_{四边形ABCD}•PD$=$\frac{{a}^{3}}{2}$=$\sqrt{2}$,∴a=$\sqrt{2}$.
∴PC=PD=BC=$\sqrt{2}$a=2,
∴S△PBC=$\frac{\sqrt{3}}{4}×4$=$\sqrt{3}$,
又S△ABC=$\frac{1}{2}×AB×BD$=2,∴VP-ABC=$\frac{1}{3}{S}_{△ABC}•PD$=$\frac{2\sqrt{2}}{3}$,
设A到平面PBC的距离为h,则VA-PBC=$\frac{1}{3}{S}_{△PBC}•h$=$\frac{\sqrt{3}}{3}h$.
∵VP-ABC=VA-PBC,∴$\frac{\sqrt{3}}{3}$h=$\frac{2\sqrt{2}}{3}$,
解得h=$\frac{2\sqrt{6}}{3}$.
点评 本题考查了线面垂直、面面垂直的判定,棱锥的体积计算,点到平面的距离计算,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x±y=0 | B. | $x±\sqrt{3}y=0$ | C. | $\sqrt{3}x±y=0$ | D. | 2x±y=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{3}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,2) | B. | (0,2] | C. | (1,2) | D. | (1,2] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{10}$ | B. | $\frac{1}{5}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | “x<-2”是“x2+3x+2>0”的必要不充分条件 | |
| B. | 对于命题p:?x0∈R,使得${x_0}^2+{x_0}-1<0$,则¬p:?x∈R,均有x2+x-1≥0 | |
| C. | 命题“若x2-3x+2=0,则x=2”的否命题为若x2-3x+2=0,则x≠2 | |
| D. | 若p∧q为假命题,则p,q均为假命题 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{2}{5}+\frac{1}{5}i$ | B. | $\frac{2}{5}-\frac{1}{5}i$ | C. | $\frac{2}{5}+\frac{1}{5}i$ | D. | $-\frac{2}{5}-\frac{1}{5}i$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com