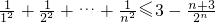解:(I)由f(x)=
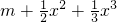
,f′(x)=x+x
2①曲线y=f(x)上的点P(1,f(1))为切点的切线的斜率k=f′(1)=2
②f′(x)=x+x
2=x(x+1)
由f′(x)<0得-1<x<0
由f′(x)>0得x<-1或x>0
∵函数f(x)在x=x
1处取得极大值,在x=x
2处取得极小值,且点(x
1,f(x
1))在第二象限,点(x
2,f(x
2))位于y轴负半轴上
∴f(-1)>0,f(0)<0
∴
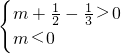
∴
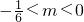
(II)f′(x)=a
1+2a
2x+3a
3x
2+4a
4x
3+…+(n+1)a
n+1x
n,
∵f′(1)=a
1+2a
2+3a
3+4a
4+…+(n+1)a
n+1=
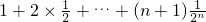
①

f′(1)=
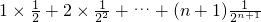
②
①-②:

f′(1)=
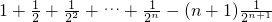
=
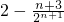
∴f′(1)=
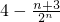
要证:T
n≤f'(1)-1.
即证:
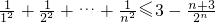
当n=1时,T
1=f'(1)-1=1
当n=2时,
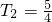
,f'(1)-1=

,∴T
n<f'(1)-1
当n≥3时,
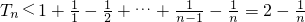
而
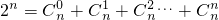
≥
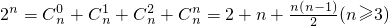
∵n≥3,∴n(n-1)>2,∴
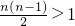
,∴2
n>n+3
∴
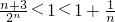
∴
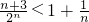
∴
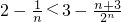
∴当n≥3时,
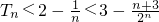
=f'(1)-1.
∴T
n≤f'(1)-1恒成立.
分析:(I)①由f(x)=
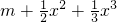
,可得f′(x)=x+x
2,从而可求曲线y=f(x)上的点P(1,f(1))为切点的切线的斜率;
②f′(x)=x+x
2=x(x+1),根据f′(x)<0得-1<x<0,f′(x)>0得x<-1或x>0,利用函数f(x)在x=x
1处取得极大值,在x=x
2处取得极小值,且点(x
1,f(x
1))在第二象限,点(x
2,f(x
2))位于y轴负半轴上,可得f(-1)>0,f(0)<0,从而可
求m的取值范围;
(II)先求导函数f′(x)=a
1+2a
2x+3a
3x
2+4a
4x
3+…+(n+1)a
n+1x
n,再利用错位相减法求得f′(1)=
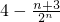
,进而分类讨论可证
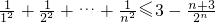
点评:本题以函数为载体,考查导数的几何意义,考查函数的极值,同时考查数列与不等式的综合,难度较大,尤其(II)学生觉得无从下手.

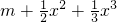 .
. 时,设函数f(x)的导函数为f'(x),令Tn=
时,设函数f(x)的导函数为f'(x),令Tn= ,证明:Tn≤f'(1)-1.
,证明:Tn≤f'(1)-1.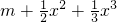 ,f′(x)=x+x2
,f′(x)=x+x2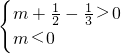
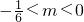
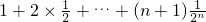 ①
① f′(1)=
f′(1)=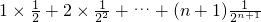 ②
② f′(1)=
f′(1)=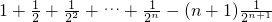 =
=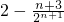
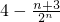
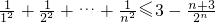
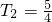 ,f'(1)-1=
,f'(1)-1= ,∴Tn<f'(1)-1
,∴Tn<f'(1)-1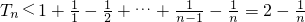
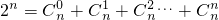 ≥
≥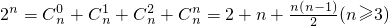
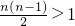 ,∴2n>n+3
,∴2n>n+3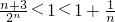
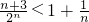
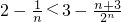
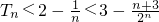 =f'(1)-1.
=f'(1)-1.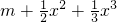 ,可得f′(x)=x+x2,从而可求曲线y=f(x)上的点P(1,f(1))为切点的切线的斜率;
,可得f′(x)=x+x2,从而可求曲线y=f(x)上的点P(1,f(1))为切点的切线的斜率;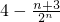 ,进而分类讨论可证
,进而分类讨论可证