
���� ��1������f��x��=x3��[a��b]�ϵġ�1������������Ϻ����ĵ����Խ������̹�ϵ���ɣ�
��2������g��x���ĵ����Խ������̹�ϵ������⼴�ɣ�
��3�����һԪ���κ��������ʣ����۶Գ����λ�ý������̹�ϵ���ɣ�
��� �⣺��1��������f��x��=x3��[a��b]�ϵġ�1���������������������ٳ���a��b����a��b������[a��b]⊆D����ʹf��x����[a��b]�ϵ�ֵ��Ϊ[a��b]
�ߺ���f��x��=x3��[a��b]�ϵĵ���������
��$\left\{\begin{array}{l}{{a}^{3}=a}\\{{b}^{3}=b}\end{array}\right.$����a=-1��b=0��a=-1��b=1����a=0��b=1��
��2��������g��x��=$\frac{1}{x+2}$��x��-2��������[a��b]�ϵ��ǡ�k�����Ρ�������
�ߺ���g��x��=$\frac{1}{x+2}$��x��-2��������[a��b]�ϵ��Ǽ�������
��$\left\{\begin{array}{l}{g��a��=kb}\\{g��b��=ka}\end{array}\right.$����$\left\{\begin{array}{l}{\frac{1}{a+2}=kb}\\{\frac{1}{b+2}=ka}\end{array}\right.$����ʽ�����$\frac{b+2}{a+2}=\frac{b}{a}$����ab+2a=ab+2b��
��2a=2b����a=b����b��aì�ܣ��ʲ����ڳ���a��b������k��ʹ����g��x��=$\frac{1}{x+2}$��x��-2��������[a��b]�ϵ��ǡ�k�����Ρ�������
��3����h��x��=-2x2-x��[a��b]�ϵġ�3�����Ρ�������
�����㺯��h��x��=-2��x+$\frac{1}{4}$��2+$\frac{1}{8}$��[a��b]�ϵ�ֵ��Ϊ[3a��3b]��
�ٵ�a��b��-$\frac{1}{4}$ʱ��h��x����[a��b]�ϵ���������ֵ��Ϊ[h��a����h��b��]����h��a��=3a��h��b��=3b��
��a��b��h��x��=3x����������ʵ������-2x2-x=3x��x2+2x=0�����x=0��x=-2��
��a=-2��b=0������������
�ڵ�-$\frac{1}{4}$��a��bʱ��h��x����[a��b]�ϵ����ݼ���ֵ��Ϊ[h��b����h��a��]����h��a��=3b��h��b��=3a��
��$\left\{\begin{array}{l}{a+b=1}\\{{a}^{2}+{b}^{2}=-2}\end{array}\right.$���������⣮
�۵�a��-$\frac{1}{4}$��bʱ����x=-$\frac{1}{4}$ʱ�����������ֵΪ$\frac{1}{8}$����3b=$\frac{1}{8}$�����b=$\frac{1}{24}$��
h��$\frac{1}{24}$��=h��-$\frac{13}{24}$����
�൱a��-$\frac{13}{24}$��h��a��=3a�����a=-2��
����a=-2��b=$\frac{1}{24}$��
���� ���⿼�����¶����ͺ�����������������������������Ե�Ӧ�ã�ת�������˼�뷽����


 �����̸�Ӯ����ٸ�Ч�����ܸ�ϰ���ϿƼ�������ϵ�д�
�����̸�Ӯ����ٸ�Ч�����ܸ�ϰ���ϿƼ�������ϵ�д� �����ҵ�����������ѧ���ӳ�����ϵ�д�
�����ҵ�����������ѧ���ӳ�����ϵ�д� ����ѧ��Ӯ�����ϵ�д�
����ѧ��Ӯ�����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1 | B�� | 2 | C�� | 3 | D�� | 4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��0��2�� | B�� | ��-2��0�� | C�� | ��0��1�� | D�� | ��-1��0�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
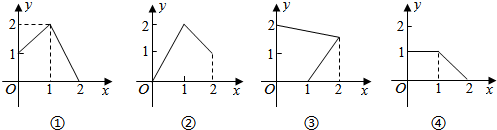
| A�� | 1�� | B�� | 2�� | C�� | 3�� | D�� | 4�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -2 | B�� | 0 | C�� | 1 | D�� | 2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 10 | B�� | 9 | C�� | 6 | D�� | 4 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com