练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】函数y=x3﹣2ax+a在（1，2）内有极小值，则实数a的取值范围是（ ）
    A.（0， ）
    B.（0，3）
    C.（ ，6）
    D.（0，6）

    【答案】C
    【解析】解：对于函数y=x3﹣2ax+a，求导可得y′=3x2﹣2a， ∵函数y=x3﹣2ax+a在（1，2）内有极小值，
    ∴y′=3x2﹣2a=0，则其有一根在（1，2）内，
    a＞0时，3x2﹣2a=0两根为± ，
    若有一根在（1，2）内，则1＜ ＜2，
    即 ＜a＜6，
    a=0时，3x2﹣2a=0两根相等，均为0，f（x）在（1，2）内无极小值，
    a＜0时，3x2﹣2a=0无根，f（x）在（1，2）内无极小值，
    综合可得， ＜a＜6，
    故选：C．
    【考点精析】根据题目的已知条件，利用函数的极值与导数的相关知识可以得到问题的答案，需要掌握求函数的极值的方法是:（1）如果在附近的左侧,右侧,那么是极大值（2）如果在附近的左侧,右侧,那么是极小值．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知在四棱锥P﹣ABCD中，底面ABCD是矩形，且AD=2，AB=1，PA⊥平面ABCD，E、F分别是线段AB、BC的中点．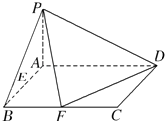
    （Ⅰ）证明：PF⊥FD；
    （Ⅱ）判断并说明PA上是否存在点G，使得EG∥平面PFD；
    （Ⅲ）若PB与平面ABCD所成的角为45°，求二面角A﹣PD﹣F的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在直角坐标系中，曲线的参数方程为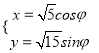（为参数），直线的参数方程为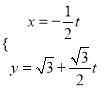（为参数）.以原点为极点， 轴的正半轴为极轴建立极坐标系，点的极坐标方程为.

    （1）求点的直角坐标，并求曲线的普通方程；

    （2）设直线与曲线的两个交点为，求的值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】定义在R上的偶函数f（x），满足f（x+1）=f（x﹣1），且f（x）在[﹣3，﹣2]上是增函数，又α、β是锐角三角形的两个内角，则（ ）
    A.f（sinα）＞f（cosβ）
    B.f（cosα）＜f（cosβ）
    C.f（sinα）＜f（cosβ）
    D.f（sinα）＜f（sinβ）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】若函数f（x）=﹣ eax（a＞0，b＞0）的图象在x=0处的切线与圆x2+y2=1相切，则a+b的最大值是（ ）
    A.4
    B.2
    C.2
    D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】学校将高二年级某班级50位同学期中考试数学成绩（均为整数）分为7组进行统计，得到如图所示的频率分布直方图.观察图中信息，回答下列问题.

    （Ⅰ）试估计该班级同学数学成绩的平均分；

    （Ⅱ）先准备从该班级数学成绩不低于130分的同学中随机选出2人参加某活动，求选出的两人在同一组的概率.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=x3﹣ax2﹣3x．
    （1）若a=4时，求f（x）在x∈[1，4]上的最大值和最小值；
    （2）若f（x）在x∈[2，+∞]上是增函数，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】下列函数中，既是偶函数，又在区间上单调递减的是

    A． B．

    C． D．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】函数f（x）= +lg（x+2）的定义域为（ ）
    A.（﹣2，1）
    B.（﹣2，1]
    C.[﹣2，1）
    D.[﹣2，﹣1]

    查看答案和解析>>

    同步练习册答案