
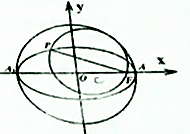
 (1)设P是椭圆M:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$上任意一点,P是焦点.证明:以PF为直径的圆与以椭圆长轴为直径的圆相切;
(1)设P是椭圆M:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$上任意一点,P是焦点.证明:以PF为直径的圆与以椭圆长轴为直径的圆相切;分析 (1)画出图形,利用三角形的中位线与椭圆的定义,推出两个圆的圆心距与半径关系,证得结果;
(2)利用双曲线的定义,通过圆心距判断出当点P分别在左、右两支时,利用两圆圆心距离和半径之间的关系判断两圆相内切、外切.
解答 (1)证明:如图,∵P是椭圆M:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$上任意一点,F为其右焦点,则以PF为直径的圆的半径是$\frac{1}{2}$|PF|,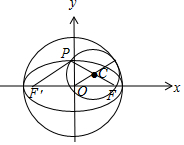 以长轴为直径的圆的半径为a,设椭圆左焦点为F′,
以长轴为直径的圆的半径为a,设椭圆左焦点为F′,
OC∥PF′,OC=$\frac{1}{2}$PF′.圆心距|OC|=$\frac{1}{2}$PF′,
∵|OC|+$\frac{1}{2}$|PF|=a,∴两个圆相内切;
(2)结论:设P是双曲线M:$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0,b>0})$上任意一点,F是焦点,
则以线段PF为直径的圆与以实轴为直径的圆相切.
证明:设以实轴|F1F2|为直径的圆的圆心为O1,其半径r1=a,
线段PF2为直径的圆的圆心为O2,其半径为r2=$\frac{|P{F}_{2}|}{2}$,
当P在双曲线左支上时,|O1O2|=$\frac{|P{F}_{1}|}{2}$,
∵r2-|O1O2|=$\frac{|P{F}_{2}|}{2}-\frac{|P{F}_{1}|}{2}$=a=r1,
∴两圆内切;
当P在双曲线右支上时,
|O1O2|=$\frac{|P{F}_{1}|}{2}$,
∵|O1O2|-r2=$\frac{|P{F}_{1}|}{2}-\frac{|P{F}_{2}|}{2}$=a=r1,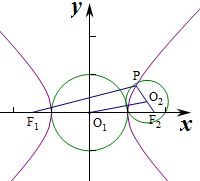
∴r1+r2=|O1O2|,
∴两圆外切.
点评 本题主要考查椭圆与双曲线的性质的应用以及两圆位置关系的判断,利用椭圆与双曲线的定义结合两圆位置关系的定义是解决本题的关键,是中档题.


 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案科目:高中数学 来源: 题型:填空题
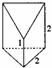 如图是底面边长为2,高为2的正三棱柱除去上面的一个高为1的三棱锥后剩下的部分构成的几何体的直观图,则该几何体的体积为$\frac{5\sqrt{3}}{3}$.
如图是底面边长为2,高为2的正三棱柱除去上面的一个高为1的三棱锥后剩下的部分构成的几何体的直观图,则该几何体的体积为$\frac{5\sqrt{3}}{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
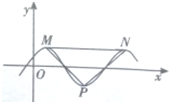 函数f(x)=$\frac{1}{2}$sin($\frac{1}{2}$ωx+$\frac{π}{6}$)(ω>0,)x∈R的部分图象如图所示,设M,N是图象上的最高点,P是图象上的最低点,若△PMN为等腰直角三角形,则ω=2π.
函数f(x)=$\frac{1}{2}$sin($\frac{1}{2}$ωx+$\frac{π}{6}$)(ω>0,)x∈R的部分图象如图所示,设M,N是图象上的最高点,P是图象上的最低点,若△PMN为等腰直角三角形,则ω=2π.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com