
分析 首先对向量$\overrightarrow{AD}$利用三角形对应边$\overrightarrow{AB},\overrightarrow{AC}$表示,然后根据向量相等得到对应系数.
解答 解:由题意,$\overrightarrow{AD}$=$\overrightarrow{AB}+\overrightarrow{BD}$=$\overrightarrow{AB}+4\overrightarrow{CD}$=$\overrightarrow{AB}+4(\overrightarrow{AD}-\overrightarrow{AC})$
,所以$3\overrightarrow{AD}=-\overrightarrow{AB}+4\overrightarrow{AC}$,
所以$\overrightarrow{AD}=-\frac{1}{3}\overrightarrow{AB}+\frac{4}{3}\overrightarrow{AC}$=m$\overrightarrow{AB}$+n$\overrightarrow{AC}$,
所以$m=-\frac{1}{3},n=\frac{4}{3}$;
故答案为:$m=-\frac{1}{3},n=\frac{4}{3}$.
点评 本题考查了向量的三角形法则以及向量相等的充要条件;属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | f(x)=$\sqrt{{x}^{2}}$ | B. | f(x)=$\root{3}{{x}^{3}}$ | C. | f(x)=($\sqrt{x}$)2 | D. | f(x)=$\frac{{x}^{2}}{x}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
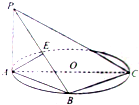 PA垂直于⊙O所在平面,B在⊙O上,AC是直径,AE⊥BP于E点
PA垂直于⊙O所在平面,B在⊙O上,AC是直径,AE⊥BP于E点查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若x2≥1,则x≥1或x≤-1;假命题 | B. | 若-1<x<1,则x2<1;假命题 | ||
| C. | 若x>1或x<-1,则x2>1;真命题 | D. | 若x≥1或x≤-1,则x2≥1;真命题 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com