
在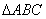 中,内角A,B,C的对边分别为
中,内角A,B,C的对边分别为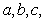 且
且 ,b=2,求A的值。
,b=2,求A的值。
科目:高中数学 来源: 题型:解答题
如图,在某点B处测得建筑物AE的顶端A的仰角为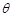 ,沿BE方向前进30m,至点C处测得顶端A的仰角为2
,沿BE方向前进30m,至点C处测得顶端A的仰角为2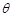 ,再继续前进10
,再继续前进10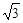 m至D点,测得顶端A的仰角为4
m至D点,测得顶端A的仰角为4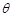 ,求建筑物AE的高度。
,求建筑物AE的高度。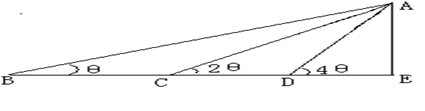
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
在海岸 处,发现北偏东
处,发现北偏东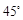 方向,距
方向,距 为
为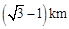 的
的 处有一艘走私船,在
处有一艘走私船,在 处北偏西
处北偏西 方向,距
方向,距 为
为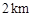 的
的 处的缉私船奉命以
处的缉私船奉命以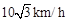 的速度追截走私船,此时走私船正以
的速度追截走私船,此时走私船正以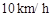 的速度从
的速度从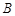 处向北偏东
处向北偏东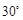 方向逃窜,问缉私船沿什么方向能最快追上走私船,并求出所需要的时间. (
方向逃窜,问缉私船沿什么方向能最快追上走私船,并求出所需要的时间. (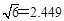 )
)
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
设矩形ABCD(AB>AD)的周长为24,把它关于AC折起来,AB折过去后交CD于点P,如图,设AB=x,求△ADP的面积的最大值,及此时x的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com