
设矩形ABCD(AB>AD)的周长为24,把它关于AC折起来,AB折过去后交CD于点P,如图,设AB=x,求△ADP的面积的最大值,及此时x的值.
△ADP面积的最大值为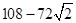 ,此时
,此时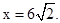
解析试题分析:22、(12分)∵AB=x,∴AD=12-x,又DP=PB′,AP=AB′-PB′=AB-DP,即AP=x-DP,
∴(12-x)2+PD2=(x-PD)2,得PD=12-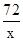 ,∵AB>AD,∴6<x<12,∴△ADP的面积S=
,∵AB>AD,∴6<x<12,∴△ADP的面积S=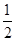 AD·DP
AD·DP
=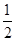 (12-x)(12-
(12-x)(12-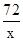 )=108-6(x+
)=108-6(x+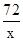 )≤108-6·
)≤108-6·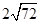 =108-
=108-
当且仅当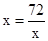 即
即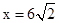 时取等号,∴△ADP面积的最大值为
时取等号,∴△ADP面积的最大值为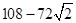 ,此时
,此时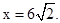
考点:本题主要考查函数模型,应用导数研究函数的最值,均值定理的应用。
点评:中档题,利通过分析图形特征,构建函数模型,再利用导数研究函数的最值,后利用均值定理确定函数的最值,从而解决实际问题。属于常见题目。本解法应用均值定理求函数的最值,应注意“一正,二定,三相等”缺一不可。


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com