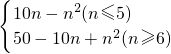已知数列{an}的前n项和Sn=10n-n2(n∈N*),又bn=|an|(n∈N*),求{bn}的前n项和Tn.
解:由S
n=10n-n
2可得S
n-1=10(n-1)-(n-1)
2,(n≥2)
两式相减可得a
n=11-2n
∵n=1时,a
1=S
1=10-1=9,满足上式
∴a
n=11-2n,∴b
n=|11-2n|.
显然n≤5时,b
n=a
n=11-2n,T
n=10n-n
2.
n≥6时,b
n=-a
n=2n-11,
T
n=(a
1+a
2+…+a
5)-(a
6+a
7+…+a
n)=2S
5-S
n=50-10n+n
2故T
n=
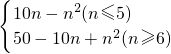
分析:由题意可得{b
n}是由一个首项为正值,而公差为负的一个等差数列,{a
n}的各项取绝对值后得到的一个新数列,因此求{b
n}的前n项和可转化为求数列{a
n}的和的问题.
点评:本题考查数列的通项与求和,考查学生分析解决问题的能力,属于中档题.