练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知函数f（x）的定义域为R，则下列命题中：?
    ①若f（x-2）是偶函数，则函数f（x）的图象关于直线x=2对称；?②若f（x+2）=-f（x-2），则函数f（x）的图象关于原点对称；?③函数y=f（2+x）与函数y=f（2-x）的图象关于直线x=2对称；?④函数y=f（x-2）与函数y=f（2-x）的图象关于直线x=2对称．?
    其中正确的命题序号是________．?

    ④
    分析：①由函数图象的变化规律知，f（x-2）的图象是由f（x）的图象向右平移两个单位
    ②由f（x+2）=-f（x-2）变形得f（x+8）=f（x）是周期函数．?
    ③函数y=f（2+x）是由f（x）向左平移2个单位，函数y=f（2-x）的图象是由f（-x）的图象向右平移2个单位，可得．④特殊图象法，函数f（x-2）是由f（x）的图象向右平移两个单位，函数y=f（2-x）的图象是由f（-x）的图象向右平移两个单位．
    解答：①不正确．因为f（x-2）的图象是由f（x）的图象向右平移两个单位而得到，结合f（x-2）是偶函数知，f（x）的图象关于x=-2对称，
    ?②由f（x+2）=-f（x-2）变形得f（x+8）=f（x）是周期函数．不能得出函数f（x）的图象关于原点对称，故不正确．?
    ③不正确，因为函数y=f（2+x）是由f（x）向左平移2个单位，函数y=f（2-x）的图象是由f（-x）的图象向右平移2个单位，故两函数的图象仍然关于原点对称．

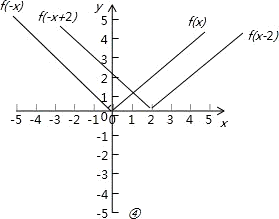
    ?④如图所示，正确．
    故答案为：④
    点评：本题主要考查函数的图象及其图象间的变换，对于常见的类型如：f（x+2）=f（2-x），f（x+2）=-f（2-x），f（x+2）=f（x-2），y=f（x+2）与y=f（2-x）间的关系，要熟练掌握．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    已知函数f（x）=log3
    		3
    x
    1-x
    ，M(x1，y1)，N(x2，y2)    是f（x）图象上的两点，横坐标为
    1
    2
    的点P满足2
    OP
    =
    OM
    +
    ON
    （O为坐标原点）．
    （Ⅰ）求证：y1+y2为定值；
    （Ⅱ）若Sn=f(
    1
    n
    )+f(
    2
    n
    )+…+f(
    n-1
    n
    )    ，其中n∈N*，且n≥2，求Sn；
    （Ⅲ）已知an=
    1
    6
    ，                          n=1
    1
    4(Sn+1)(Sn+1+1)
    ，n≥2
    ，其中n∈N*，Tn为数列{an}的前n项和，若Tn＜m（Sn+1+1）对一切n∈N*都成立，试求m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    下列说法正确的有（　　）个．
    ①已知函数f（x）在（a，b）内可导，若f（x）在（a，b）内单调递增，则对任意的?x∈（a，b），有f′（x）＞0．
    ②函数f（x）图象在点P处的切线存在，则函数f（x）在点P处的导数存在；反之若函数f（x）在点P处的导数存在，则函数f（x）图象在点P处的切线存在．
    ③因为3＞2，所以3+i＞2+i，其中i为虚数单位．
    ④定积分定义可以分为：分割、近似代替、求和、取极限四步，对求和In=
    n
    i=1
    f(ξi)△x    中ξi的选取是任意的，且In仅于n有关．
    ⑤已知2i-3是方程2x2+px+q=0的一个根，则实数p，q的值分别是12，26．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知函数f（x）=sin（2x-
    π
    6
    ），g（x）=sin（2x+
    π
    3
    ），直线y=m与两个相邻函数的交点为A，B，若m变化时，AB的长度是一个定值，则AB的值是（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （Ⅰ）已知函数f（x）=x3-x，其图象记为曲线C．
    （i）求函数f（x）的单调区间；
    （ii）证明：若对于任意非零实数x1，曲线C与其在点P1（x1，f（x1））处的切线交于另一点P2（x2，f（x2）），曲线C与其在点P2（x2，f（x2））处的切线交于另一点P3（x3，f（x3）），线段P1P2，P2P3与曲线C所围成封闭图形的面积记为S1，S2．则
    S1S2
    为定值；
    （Ⅱ）对于一般的三次函数g（x）=ax3+bx2+cx+d（a≠0），请给出类似于（Ⅰ）（ii）的正确命题，并予以证明．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知函数f（x）=x3-ax+b存在极值点．
    （1）求a的取值范围；
    （2）过曲线y=f（x）外的点P（1，0）作曲线y=f（x）的切线，所作切线恰有两条，切点分别为A、B．
    （ⅰ）证明：a=b；
    （ⅱ）请问△PAB的面积是否为定值？若是，求此定值；若不是求出面积的取值范围．

    查看答案和解析>>

    同步练习册答案