
 ;
;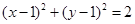 ,表示以(1,1)为圆心,
,表示以(1,1)为圆心,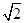 为半径的圆.
为半径的圆. 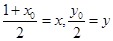 ,
,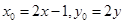 ,然后将B的坐标代入圆C的方程即可得到M的轨迹方程,再通过方程可判断出M的轨迹也是圆.
,然后将B的坐标代入圆C的方程即可得到M的轨迹方程,再通过方程可判断出M的轨迹也是圆.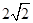 …………………5分
…………………5分 ……………………………………6分
……………………………………6分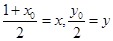 ,……………………8分
,……………………8分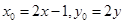 ,代入圆C方程得
,代入圆C方程得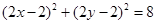 ,…………10分
,…………10分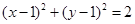 ……………11分
……………11分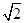 为半径的圆.………12分
为半径的圆.………12分

科目:高中数学 来源:不详 题型:解答题
 和圆外一点
和圆外一点 .
. 作圆的割线交圆于
作圆的割线交圆于 两点,若|
两点,若| |=4,求直线
|=4,求直线 的方程;
的方程; 作圆的切线,切点为
作圆的切线,切点为 ,求切线长及
,求切线长及 所在直线的方程.
所在直线的方程.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
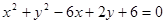 ,则其圆心坐标和半径分别为( )
,则其圆心坐标和半径分别为( )| A.(3, -1),r = 4 | B.(3, -1),r = 2 |
| C.(-3, 1),r = 2 | D.(-3, 1),r = 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com