
分析 (1)由题意,得$\left\{\begin{array}{l}{c=2}\\{a=\sqrt{5}}\end{array}\right.$,由此能求出椭圆W的方程.
(2)设直线AC:y=kx+m,A(x1,y1),C(x2,y2),AC的中点M(x0,y0),B(x3,y3),直线代入抛物线方程可得(1+5k2)x2+10kmx+5m2-5=0,由此利用根的判别式、韦达定理、椭圆性质,结合已知条件能推导出四边形OABC可以为矩形.
解答 解:(1)∵椭圆W:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),短轴端点到其右焦点F(2,0)的距离为$\sqrt{5}$,
∴由题意,得$\left\{\begin{array}{l}{c=2}\\{a=\sqrt{5}}\end{array}\right.$,∴b=$\sqrt{{a}^{2}-{c}^{2}}$=1,
∴椭圆W的方程为$\frac{{x}^{2}}{5}$+y2=1.
(2)设直线AC:y=kx+m,A(x1,y1),C(x2,y2),AC的中点M(x0,y0),B(x3,y3),
直线代入抛物线方程可得(1+5k2)x2+10kmx+5m2-5=0,
∴△=(10km)2-4(1+5k2)(5m2-5)>0,
x1+x2=-$\frac{10km}{1+5{k}^{2}}$,x1x2=$\frac{5{m}^{2}-5}{1+5{k}^{2}}$.①由条件OA⊥OC,得x1x2+y1y2=0,
即x1x2+(kx1+m)(kx2+m)=0,
整理得(1+k2)x1x2+km(x1+x2)+m2=0,
将(1)式代入得6m2=5k2+5,②
又x0=$\frac{{x}_{1}+{x}_{2}}{2}$=-$\frac{5km}{1+5{k}^{2}}$,y0=kx0+m=$\frac{m}{1+5{k}^{2}}$,
且M同时也是OB的中点,∴x3=2x0,y3=2y0,
∵B在椭圆上,∴${{x}_{3}}^{2}+5{{y}_{3}}^{2}$=5,
即$4{{x}_{0}}^{2}+20{{y}_{0}}^{2}=5$,代入整理可得4m2=5k2+1,③
由②③解得m2=2,k2=$\frac{7}{5}$,
验证知△=120>0,
∴四边形OABC可以为矩形.
点评 本题考查椭圆方程的求法,考查四边形能否为矩形的判断,是中档题,解题时要认真审题,注意根的判别式、韦达定理、椭圆性质的合理运用.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 真,假,假 | B. | 真,真,假 | C. | 真,假,真 | D. | 假,假,真 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | m>$\frac{5}{4}$ | B. | m<-$\frac{3}{4}$ | C. | m>1 | D. | m>-$\frac{3}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
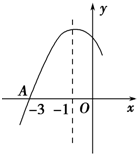 如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(-3,0),对称轴为x=-1.给出下面四个结论:
如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(-3,0),对称轴为x=-1.给出下面四个结论:| A. | ②④ | B. | ①④ | C. | ②③ | D. | ①③ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com