
分析 利用导数的几何意义即可得到切线的斜率,得出切线的方程,利用方程求出与x轴交点的横坐标,再利用导数研究函数的单调性、极值、最值即可.
解答 解:设切点为(x0,${{x}_{0}}^{2}{e}^{-{x}_{0}}$),
则切线方程为y-${{x}_{0}}^{2}{e}^{-{x}_{0}}$=${e}^{-{x}_{0}}$($2{x}_{0}-{{x}_{0}}^{2}$)(x-x0),
令y=0,解得x=(x0-2)+$\frac{2}{{x}_{0}-2}$+3,
∵曲线y=f(x)的切线l的斜率为负数,
∴${e}^{-{x}_{0}}$($2{x}_{0}-{{x}_{0}}^{2}$)<0,
∴x0<0或x0>2,
令f(x0)=(x0-2)+$\frac{2}{{x}_{0}-2}$+3,
则f′(x0)=$\frac{({{x}_{0}}^{2}-2)^{2}-2}{({{x}_{0}}^{2}-2)^{2}}$.
①当x0<0时,$({x}_{0}-2)^{2}-2$>0,即f′(x0)>0,
∴f(x0)在(-∞,0)上单调递增,∴f(x0)<f(0)=0;
②当x0>2时,令f′(x0)=0,解得x0=2+$\sqrt{2}$.
当x0>2+$\sqrt{2}$时,f′(x0)>0,函数f(x0)单调递增;
当2<x0<2+$\sqrt{2}$时,f′(x0)<0,函数f(x0)单调递减.
故当x0=2+$\sqrt{2}$时,函数f(x0)取得极小值,也即最小值,且f(2+$\sqrt{2}$)=2 $\sqrt{2}$+3.
综上可知:切线l在x轴上截距的取值范围是(-∞,0)∪[2 $\sqrt{2}$+3,+∞).
故答案为(-∞,0)∪[2 $\sqrt{2}$+3,+∞).
点评 本题考查利用导数研究函数的单调性、切线、函数的值域,综合性强,考查了推理能力和计算能力.


 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 16 | B. | 8 | C. | 10 | D. | 没有最小值 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
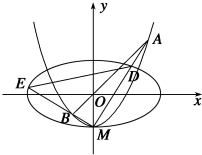 如图,椭圆C1:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$═1(a>b>0)的离心率为$\frac{\sqrt{3}}{2}$,x轴被曲线C2:y=x2-b截得的线段长等于C1的长半轴长.C2与y轴的交点为M,过坐标原点O的直线l与C2相交于点A,B,两直线MA,MB分别与C1相交于点D,E.
如图,椭圆C1:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$═1(a>b>0)的离心率为$\frac{\sqrt{3}}{2}$,x轴被曲线C2:y=x2-b截得的线段长等于C1的长半轴长.C2与y轴的交点为M,过坐标原点O的直线l与C2相交于点A,B,两直线MA,MB分别与C1相交于点D,E.| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com