
分析 (1)利用作差法,即可证明不等式;
(2)利用柯西不等式,可得$y=2×\sqrt{x-3}+4×\sqrt{5-x}≤\sqrt{({2^2}+{4^2})[{{(\sqrt{x-3})}^2}+{{(\sqrt{5-x})}^2}]}$,即可得出结论.
解答 (1)证明:(a2+b2)(c2+d2)-(ac+bd)2=a2d2+b2c2-2adbc…(2分)
=(ad-bc)2≥0,…(4分)
当且仅当ad-bc=0时,等号成立.…(5分)
(2)解:函数的定义域为[3,5],且y>0,…(6分)
则$y=2×\sqrt{x-3}+4×\sqrt{5-x}≤\sqrt{({2^2}+{4^2})[{{(\sqrt{x-3})}^2}+{{(\sqrt{5-x})}^2}]}$…(8分)
=$\sqrt{20×2}=2\sqrt{10}$,…(9分)
当且仅当$2\sqrt{5-x}=4\sqrt{x-3}$时,等号成立,
即$x=\frac{17}{5}$时函数取最大值$2\sqrt{10}$.…(10分)
点评 本题考查不等式的证明,考查柯西不等式的运用,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ∅ | B. | {0} | C. | {-1} | D. | $\{-1,\sqrt{2}\}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
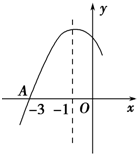 如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(-3,0),对称轴为x=-1.给出下面四个结论:
如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(-3,0),对称轴为x=-1.给出下面四个结论:| A. | ②④ | B. | ①④ | C. | ②③ | D. | ①③ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com