
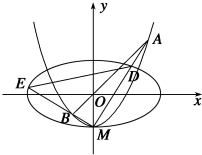
 如图,椭圆C1:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$═1(a>b>0)的离心率为$\frac{\sqrt{3}}{2}$,x轴被曲线C2:y=x2-b截得的线段长等于C1的长半轴长.C2与y轴的交点为M,过坐标原点O的直线l与C2相交于点A,B,两直线MA,MB分别与C1相交于点D,E.
如图,椭圆C1:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$═1(a>b>0)的离心率为$\frac{\sqrt{3}}{2}$,x轴被曲线C2:y=x2-b截得的线段长等于C1的长半轴长.C2与y轴的交点为M,过坐标原点O的直线l与C2相交于点A,B,两直线MA,MB分别与C1相交于点D,E.| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 ①由$\frac{c}{a}$=$\frac{\sqrt{3}}{2}$,又a2=b2+c2,可解得a=2b.在y=x2-b中,令y=0,可得2$\sqrt{b}$=a.联立解出即可得出.
②由$\left\{\begin{array}{l}{y=kx}\\{y={x}^{2}-1}\end{array}\right.$,得x2-kx-1=0,设A(x1,y1),B(x2,y2),把根与系数的关系代入$\overrightarrow{MA}•\overrightarrow{MB}$=x1x2+(y1+1)(y2+1)=0,可得MA⊥MB,即可判断出结论.
③设直线MA的斜率为k,则直线MA的方程为y=kx-1.由$\left\{\begin{array}{l}{y=kx-1}\\{y={x}^{2}-1}\end{array}\right.$,解得点A的坐标为(k,k2-1).又直线MB的斜率为-$\frac{1}{k}$,同理可得点B的坐标为$(-\frac{1}{k},\frac{1}{{k}^{2}}-1)$,于是S1=$\frac{1}{2}$|MA|•|MB|=$\frac{1+{k}^{2}}{2|k|}$.由$\left\{\begin{array}{l}{y=kx-1}\\{{x}^{2}+4{y}^{2}=4}\end{array}\right.$,得(1+4k12)x2-8k1x=0.可得点D的坐标为$(\frac{8k}{1+4{k}^{2}},\frac{4{k}^{2}-1}{1+4{k}^{2}})$.同理可得点E的坐标为$(\frac{-8k}{4+{k}^{2}},\frac{4-{k}^{2}}{4+{k}^{2}})$.于是S2=$\frac{1}{2}$|MD|•|ME|.故$\frac{{S}_{1}}{{S}_{2}}$=$\frac{1}{64}$$(4{k}^{2}+\frac{4}{{k}^{2}}+17)$.利用基本不等式的性质即可判断出结论.
④由③令$\frac{{S}_{1}}{{S}_{2}}$=$\frac{1}{64}$$(4{k}^{2}+\frac{4}{{k}^{2}}+17)$=$\frac{17}{32}$,解得k2,可得kl=$\frac{{k}^{2}-1}{k}$,即可得出.
解答 解:①∵$\frac{c}{a}$=$\frac{\sqrt{3}}{2}$,又a2=b2+c2,可解得a=2b.在y=x2-b中,令y=0,得x=$±\sqrt{b}$,∴2$\sqrt{b}$=a.
联立解得a=2,b=1.∴曲线C1,C2的方程分别为$\frac{{x}^{2}}{4}$+y2=1,y=x2-1.
②由$\left\{\begin{array}{l}{y=kx}\\{y={x}^{2}-1}\end{array}\right.$,得x2-kx-1=0,设A(x1,y1),B(x2,y2),∴x1+x2=k,x1x2=-1.
∵M(0,-1),∴$\overrightarrow{MA}•\overrightarrow{MB}$=x1x2+(y1+1)(y2+1)=x1x2+y1y2+y1+y2+1=-1-k2+k2+1=0,
∴MA⊥MB,∴MD⊥ME.
③设直线MA的斜率为k,则直线MA的方程为y=kx-1.
由$\left\{\begin{array}{l}{y=kx-1}\\{y={x}^{2}-1}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=0}\\{y=-1}\end{array}\right.$,或$\left\{\begin{array}{l}{x=k}\\{y={k}^{2}-1}\end{array}\right.$.则点A的坐标为(k,k2-1).
又直线MB的斜率为-$\frac{1}{k}$,同理可得点B的坐标为$(-\frac{1}{k},\frac{1}{{k}^{2}}-1)$,
于是S1=$\frac{1}{2}$|MA|•|MB|=$\frac{1}{2}$$\sqrt{{k}^{2}+{k}^{4}}$•$\sqrt{\frac{1}{{k}^{2}}+\frac{1}{{k}^{4}}}$=$\frac{1+{k}^{2}}{2|k|}$.
由$\left\{\begin{array}{l}{y=kx-1}\\{{x}^{2}+4{y}^{2}=4}\end{array}\right.$,得(1+4k12)x2-8k1x=0.
解得$\left\{\begin{array}{l}{x=0}\\{y=-1}\end{array}\right.$,或$\left\{\begin{array}{l}{x=\frac{8k}{1+4{k}^{2}}}\\{y=\frac{4{k}^{2}-1}{1+4{k}^{2}}}\end{array}\right.$,则点D的坐标为$(\frac{8k}{1+4{k}^{2}},\frac{4{k}^{2}-1}{1+4{k}^{2}})$.
又直线ME的斜率为-$\frac{1}{k}$.同理可得点E的坐标为$(\frac{-8k}{4+{k}^{2}},\frac{4-{k}^{2}}{4+{k}^{2}})$.
于是S2=$\frac{1}{2}$|MD|•|ME|=$\frac{32(1+{k}^{2})|k|}{(1+4{k}^{2})(4+{k}^{2})}$.故$\frac{{S}_{1}}{{S}_{2}}$=$\frac{1}{64}$$(4{k}^{2}+\frac{4}{{k}^{2}}+17)$≥$\frac{2\sqrt{4{k}^{2}×\frac{4}{{k}^{2}}}+17}{64}$=$\frac{25}{64}$,
当且仅当k2=1时取等号,因此不正确.
④由③令$\frac{{S}_{1}}{{S}_{2}}$=$\frac{1}{64}$$(4{k}^{2}+\frac{4}{{k}^{2}}+17)$=$\frac{17}{32}$,解得k2=4或$\frac{1}{4}$,
∴kl=$\frac{{k}^{2}-1}{k}$=$±\frac{3}{2}$.∴直线l的方程为:y=$\frac{3}{2}$x或y=-$\frac{3}{2}$x.正确.
综上可得:只有①②④正确.
故选:C.
点评 本题考查了椭圆与抛物线的标准方程、直线与椭圆抛物线相交问题、一元二次方程的根与系数的关系、向量数量积运算性质、三角形面积计算公式、基本不等式的性质,考查了推理能力与计算能力,属于难题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $±\frac{1}{2}$ | B. | $±\frac{{\sqrt{3}}}{2}$ | C. | $-\frac{{\sqrt{3}}}{2}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ∅ | B. | {0} | C. | {-1} | D. | $\{-1,\sqrt{2}\}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com