
| A�� | 30�� | B�� | 45�� | C�� | 60�� | D�� | 90�� |
���� ���������������������������Ķ��壬���$\overrightarrow a$��$\overrightarrow b$�ļнǦȵ�ֵ��
��� �⣺����$\overrightarrow a$��$\overrightarrow b$����|${\overrightarrow a}$|=1��|${\overrightarrow b}$|=4��$\overrightarrow a$•$\overrightarrow b$=2����$\overrightarrow a$��$\overrightarrow b$�ļн�Ϊ�ȣ��ɵ�$\overrightarrow{a}•\overrightarrow{b}$=1��4•cos��=2��
��cos��=$\frac{1}{2}$����=60�㣬
��ѡ��C��
���� ������Ҫ���������������������Ķ��壬���ڻ����⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ����f��x��=cos��2x+$\frac{��}{3}$����ͼ������ƽ��$\frac{��}{3}$����λ���ȿɵõ�y=sin2x��ͼ�� | |
| B�� | x=$\frac{��}{6}$�Ǻ���f��x����һ���Գ��� | |
| C�� | ��$\frac{��}{12}$��0���Ǻ���f��x����һ���Գ����� | |
| D�� | ����f��x��=cos��2x+$\frac{��}{3}$����[0��$\frac{��}{2}$]�ϵ���СֵΪ-$\frac{\sqrt{3}}{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
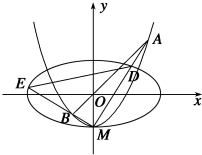 ��ͼ����ԲC1��$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$�T1��a��b��0����������Ϊ$\frac{\sqrt{3}}{2}$��x�ᱻ����C2��y=x2-b�صõ��߶γ�����C1�ij����᳤��C2��y��Ľ���ΪM��������ԭ��O��ֱ��l��C2�ཻ�ڵ�A��B����ֱ��MA��MB�ֱ���C1�ཻ�ڵ�D��E��
��ͼ����ԲC1��$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$�T1��a��b��0����������Ϊ$\frac{\sqrt{3}}{2}$��x�ᱻ����C2��y=x2-b�صõ��߶γ�����C1�ij����᳤��C2��y��Ľ���ΪM��������ԭ��O��ֱ��l��C2�ཻ�ڵ�A��B����ֱ��MA��MB�ֱ���C1�ཻ�ڵ�D��E��| A�� | 1�� | B�� | 2�� | C�� | 3�� | D�� | 4�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��-�ޣ�0�� | B�� | $��{0��\frac{3}{2e}}]$ | C�� | $[{\frac{3}{2e}��+��}��$ | D�� | $��{-�ޣ�0}����[{\frac{3}{2e}��+��}��$ |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com