
分析 (1)当A=∅时,$a<-\frac{3}{2}$,满足题意;当A≠∅,$a≥-\frac{3}{2}$时,则有$\left\{\begin{array}{l}{1-a≥-1}\\{a+4≤5}\end{array}\right.$,解得:$-\frac{3}{2}≤a≤1$.综上,a的范围可求.
(2)由A∪B=B,可得A⊆B,当A=∅时,则有1-a>a+4,即$a<-\frac{3}{2}$,满足题意;当A≠∅,即$a≥-\frac{3}{2}$时,则1-a>5或a+4<-1,求得a∈∅,取并集可得a的取值范围.
解答 解:(1)∵A={x|1-a≤x≤a+4},B={x|x<-1或x>5},且A∩B=∅,
∴当A=∅时,则有1-a>a+4,即$a<-\frac{3}{2}$,满足题意;
当A≠∅,可得1-a≤a+4,即$a≥-\frac{3}{2}$时,
则有$\left\{\begin{array}{l}{1-a≥-1}\\{a+4≤5}\end{array}\right.$,
解得:$-\frac{3}{2}≤a≤1$.
综上,a的范围为a≤1.
(2)∵A∪B=B,∴A⊆B,
当A=∅时,则有1-a>a+4,即$a<-\frac{3}{2}$,满足题意;
当A≠∅,可得1-a≤a+4,即$a≥-\frac{3}{2}$时,
依题意得:1-a>5或a+4<-1,
解得:a<-4或a<-5,则a∈∅.
综上,a的取值范围是$a<-\frac{3}{2}$.
点评 本题考查了集合的包含关系判断及应用,考查了交集及并集运算,是中档题.


 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | f(x)=sinx | B. | f(x)=-|x+1| | ||
| C. | $f(x)=ln\frac{2-x}{2+x}$ | D. | f(x)=$\frac{1}{2}$(ax+a-x),(a>0,a≠1) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
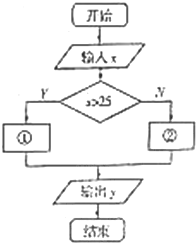 某客运部门规定甲、乙两地之间旅客托运行李的费用为:不超过25kg按0.5元/kg收费,超过25kg的部分按0.8元/kg收费,计算收费的程序框图如图所示,则①②处应填( )
某客运部门规定甲、乙两地之间旅客托运行李的费用为:不超过25kg按0.5元/kg收费,超过25kg的部分按0.8元/kg收费,计算收费的程序框图如图所示,则①②处应填( )| A. | y=0.8x y=0.5x | B. | y=0.5x y=0.8x | ||
| C. | y=25×0.5+(x-25)×0.8 y=0.5x | D. | y=25×0.5+0.8x y=0.8x |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x+y-4=0 | B. | x-y+4=0 | C. | 2x+y-6=0 | D. | x+2y-6=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=log2x | B. | $y=-\sqrt{x}$ | C. | $y={(\frac{1}{2})^x}$ | D. | $y=\frac{1}{x}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com