
分析 分类讨论二次项的系数a3与0的关系,利用二次函数的性质,求得不等式的解集.
解答 解:对于不等式a3x2-(a2+a)x+1=(ax-1)•(a2x-1)>0,
(1)当a=0时,不等式即1>0,恒成立,此时,不等式的解集为R.
(2)当a>0时,
若a=1,不等式即 x2-2x+1>0,∴x≠1,即不等式的解集为{x|x≠1}.
若0<a<1,则$\frac{1}{a}$<$\frac{1}{{a}^{2}}$,不等式a3x2-(a2+a)x+1>0的解集为 {x|x<$\frac{1}{a}$,或 x>$\frac{1}{{a}^{2}}$}.
若a>1,则$\frac{1}{a}$>$\frac{1}{{a}^{2}}$,不等式a3x2-(a2+a)x+1>0的解集为{x|x<$\frac{1}{{a}^{2}}$,或 x>$\frac{1}{a}$}.
②当a<0时,则$\frac{1}{a}$<$\frac{1}{{a}^{2}}$,不等式a3x2-(a2+a)x+1>0的解集为 {x|$\frac{1}{a}$<x<$\frac{1}{{a}^{2}}$ }.
综上可得,当a=0时,不等式的解集为R;
当a=1时,不等式的解集为{x|x≠1};
当0<a<1时,不等式的解集为{x|x<$\frac{1}{a}$,或 x>$\frac{1}{{a}^{2}}$};
当a>1时,不等式的解集为{x|x>$\frac{1}{a}$,或 x<$\frac{1}{{a}^{2}}$};
当a<0时,不等式的解集为 {x|$\frac{1}{a}$<x<$\frac{1}{{a}^{2}}$ }.
点评 本题主要考查一元二次不等式的解法,二次函数的性质,体现了分类讨论的数学思想,属于中档题.


科目:高中数学 来源: 题型:填空题
 (1)如图是一容量为100的样本的重量的频率分布直方图,则由图可估计样本重量的中位数为12.5;
(1)如图是一容量为100的样本的重量的频率分布直方图,则由图可估计样本重量的中位数为12.5;| P(K2≥k) | 0.100 | 0.050 | 0.010 |
| k | 2.706 | 3.841 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 函数f(x)=cos(2x+$\frac{π}{3}$)的图象向右平移$\frac{π}{3}$个单位长度可得到y=sin2x的图象 | |
| B. | x=$\frac{π}{6}$是函数f(x)的一个对称轴 | |
| C. | ($\frac{π}{12}$,0)是函数f(x)的一个对称中心 | |
| D. | 函数f(x)=cos(2x+$\frac{π}{3}$)在[0,$\frac{π}{2}$]上的最小值为-$\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
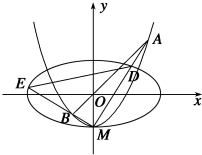 如图,椭圆C1:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$═1(a>b>0)的离心率为$\frac{\sqrt{3}}{2}$,x轴被曲线C2:y=x2-b截得的线段长等于C1的长半轴长.C2与y轴的交点为M,过坐标原点O的直线l与C2相交于点A,B,两直线MA,MB分别与C1相交于点D,E.
如图,椭圆C1:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$═1(a>b>0)的离心率为$\frac{\sqrt{3}}{2}$,x轴被曲线C2:y=x2-b截得的线段长等于C1的长半轴长.C2与y轴的交点为M,过坐标原点O的直线l与C2相交于点A,B,两直线MA,MB分别与C1相交于点D,E.| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | $-\frac{{\sqrt{2}}}{2}$ | C. | 0 | D. | $\frac{{\sqrt{2}}}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com