
| A. | $\sqrt{2}$ | B. | $-\frac{{\sqrt{2}}}{2}$ | C. | 0 | D. | $\frac{{\sqrt{2}}}{2}$ |
分析 f(n)=cos($\frac{nπ}{2}$+$\frac{π}{4}$),可得f(n+4)=$cos(\frac{n+4}{2}π+\frac{π}{4})$=f(n),即可得出.
解答 解:∵f(n)=cos($\frac{nπ}{2}$+$\frac{π}{4}$),∴f(1)=-$\frac{\sqrt{2}}{2}$,f(2)=-$\frac{\sqrt{2}}{2}$,f(3)=$\frac{\sqrt{2}}{2}$,f(4)=$\frac{\sqrt{2}}{2}$,
f(n+4)=$cos(\frac{n+4}{2}π+\frac{π}{4})$=f(n),
∴f(1)+f(2)+…+f(2015)=[f(1)+f(2)+f(3)+f(4)]×503+f(1)+f(2)+f(3)
=0-$\frac{\sqrt{2}}{2}$
=-$\frac{\sqrt{2}}{2}$.
故选:B.
点评 本题考查了数列与三角函数的周期性、数列求和,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
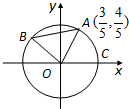 如图A、B是单位圆O上的动点,C是圆与x轴正半轴的交点,设∠AOC=α.
如图A、B是单位圆O上的动点,C是圆与x轴正半轴的交点,设∠AOC=α.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x<y<z | B. | z<x<y | C. | z<y<x | D. | y<z<x |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-2,-3) | B. | (-3,2) | C. | (-2,3) | D. | (3,2) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com