练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

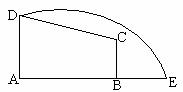
    如图, 在直角梯形ABCD中, AD∥BC, DA⊥AB, 又AD＝3, AB＝4, BC＝,E在线段AB的延长线上. 曲线DE (含两端点) 上任意一点到A、B两点的距离之和都相等.

    (1) 建立适当的坐标系, 并求出曲线DE的方程;

    (2) 过点C能否作出一条与曲线DE相交且以C点为中心的弦? 如果不能, 请说明理由;

    如果能, 请求出弦所在直线的方程.

    （1）以AB所在直线为x轴以线段AB的垂直平分线为y轴

    建立直角坐标系，则A（-2，0），B（2，0），D（-2，3），C（2，）

    所以

    因为上任意一点到A、B两点的距离之和都相等

    所以曲线DE是以A、B为焦点的椭圆的一部分

    所以长轴长，短半轴长

    所以曲线DE (含两端点)的方程为

    （2）设过点C的弦所在直线与曲线DE交于

    则      （1）

          （2）

    （1）-（2）得

    因为弦以C点为中心

    所以斜率

    所以弦所在直线的方程为

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

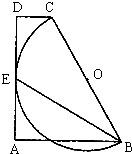    精英家教网已知：如图，在直角梯形ABCD中，AB∥CD，AD⊥AB，垂足为A，以腰BC为直径的半圆O切AD于点E，连接BE，若BC=6，∠EBC=30°，则梯形ABCD的面积为
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

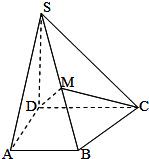    精英家教网如图，在直角梯形ABCD中，∠A=∠D=90°，AB＜CD，SD⊥平面ABCD，AB=AD=a，SD=
    		2
    a    ．
    （Ⅰ）求证：平面SAB⊥平面SAD；
    （Ⅱ）设SB的中点为M，当
    CD
    AB
    为何值时，能使DM⊥MC？请给出证明．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    如图，在直角梯形ABCP中，BC∥AP，AB⊥BC，CD⊥AP，AD=DC=PD=2．点E、F分别是PC、BD的中点，现将△PDC沿CD折起，使PD⊥平面ABCD，
    （1）求证：EF∥平面PAD；
    （2）求点A到平面PBC的距离．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

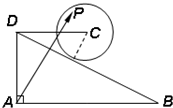    （2012•洛阳模拟）如图，在直角梯形ABCD中，AD⊥AB，AB∥DC，AD=DC=1，AB=2，动点P在以点C为圆心，且与直线BD相切的圆上或圆内移动，设
    AP
    =λ
    AD
    +μ
    AB
    （λ，μ∈R），则λ+μ取值范围是（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    精英家教网如图，在直角梯形ABCD中，AB∥CD，AB⊥AD，CD=2，AB=3，∠ABC=60°，将此梯形以AD所在直线为轴旋转一周，所得几何体的表面积是（　　）
    A、46πB、23πC、26πD、36π

    查看答案和解析>>

    同步练习册答案