
【题目】过![]() 轴正半轴上一点
轴正半轴上一点![]() 做直线与抛物线
做直线与抛物线![]() 交于
交于![]() ,
,![]() ,
,![]() 两点,且满足
两点,且满足![]() ,过定点
,过定点![]() 与点
与点![]() 做直线
做直线![]() 与抛物线交于另一点
与抛物线交于另一点![]() ,过点
,过点![]() 与点
与点![]() 做直线
做直线![]() 与抛物线交于另一点
与抛物线交于另一点![]() .设三角形
.设三角形![]() 的面积为
的面积为![]() ,三角形
,三角形![]() 的面积为
的面积为![]() .
.
(1)求正实数![]() 的取值范围;
的取值范围;
(2)连接![]() ,
,![]() 两点,设直线
两点,设直线![]() 的斜率为
的斜率为![]() ;
;
(ⅰ)当![]() 时,直线
时,直线![]() 在
在![]() 轴的纵截距范围为
轴的纵截距范围为![]() ,则求
,则求![]() 的取值范围;
的取值范围;
(ⅱ)当实数![]() 在(1)取到的范围内取值时,求
在(1)取到的范围内取值时,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() (2)(ⅰ)
(2)(ⅰ)![]() (ⅱ)
(ⅱ)![]()
【解析】
(1)设过点![]()
![]() 的直线为
的直线为![]() ,与抛物线联立可得
,与抛物线联立可得![]() ,利用韦达定理可得
,利用韦达定理可得![]() ,则可得
,则可得![]() ,代入
,代入![]() 中,进而由
中,进而由![]() 求解即可;
求解即可;
(2)(ⅰ)设过点![]() 的直线为
的直线为![]() ,过点
,过点![]() 的直线
的直线![]() ,分别与抛物线联立,利用韦达定理和直线的斜率公式可得
,分别与抛物线联立,利用韦达定理和直线的斜率公式可得![]() ,根据直线
,根据直线![]() 在
在![]() 轴的纵截距范围为
轴的纵截距范围为![]() ,即可求得
,即可求得![]() 的范围,进而得到
的范围,进而得到![]() ,即
,即![]() 的范围;
的范围;
(ⅱ)由![]() ,根据(1)和(ⅰ)求解即可.
,根据(1)和(ⅰ)求解即可.
(1)设过点![]()
![]() 的直线为
的直线为![]() ,
,
联立![]() 可得
可得![]() ,且
,且![]() ,
,
设![]() ,
,![]() ,
,
所以![]() ,则
,则![]() ,
,
因为![]() ,所以
,所以![]() ,
,
解得![]()
(2)由题,设![]() ,
,![]() ,
,![]() ,
,![]() ,
,
(ⅰ)设过点![]() 的直线为
的直线为![]() ,过点
,过点![]() 的直线
的直线![]() ,
,
联立![]() 可得
可得![]() ,
,
联立 可得
可得![]() ,
,
所以 ,
,
所以 ,
,
因为直线![]() 在
在![]() 轴的纵截距范围为
轴的纵截距范围为![]() ,设截距为
,设截距为![]() ,
,
因为![]() ,则
,则![]() ,所以
,所以![]() ,则
,则![]()
(ⅱ)![]() ,
,![]() ,
,
由(1)可知![]() ,由(ⅰ)可知
,由(ⅰ)可知![]() ,
,
因为![]() ,
,
所以![]()


科目:高中数学 来源: 题型:
【题目】新型冠状病毒蔓延以来,世界各国都在研制疫苗,某专家认为,某种抗病毒药品对新型冠状病毒具有抗病毒、抗炎作用,假如规定每天早上7:00和晚上7:00各服药一次,每次服用该药药量700毫克具有抗病毒功效,若人的肾脏每12小时从体内滤出这种药的70%,该药在人体内含量超过1000毫克,就将产生副作用,若人长期服用这种药,则这种药__________(填“会”或者“不会”)对人体产生副作用.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线![]() 的极坐标方程是
的极坐标方程是![]() ,以极点为原点,极轴为
,以极点为原点,极轴为![]() 轴非负半轴建立平面直角坐标系,直线
轴非负半轴建立平面直角坐标系,直线![]() 的参数方程为
的参数方程为 (
(![]() 为参数).
为参数).
(1)写出曲线![]() 的直角坐标方程和直线
的直角坐标方程和直线![]() 的普通方程;
的普通方程;
(2)在(1)中,设曲线![]() 经过伸缩变换
经过伸缩变换 得到曲线
得到曲线![]() ,设曲线
,设曲线![]() 上任意一点为
上任意一点为![]() ,当点
,当点![]() 到直线
到直线![]() 的距离取最大值时,求此时点
的距离取最大值时,求此时点![]() 的直角坐标.
的直角坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() ,曲线
,曲线![]() (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,以
为极点,以![]() 轴的正半轴为极轴建立极坐标系.
轴的正半轴为极轴建立极坐标系.
(1)求![]() 的极坐标方程;
的极坐标方程;
(2)射线![]() 的极坐标方程为
的极坐标方程为![]() ,若
,若![]() 分别与
分别与![]() 交于异于极点的
交于异于极点的![]() 两点,求
两点,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,且经过点
,且经过点![]() ,两个焦点分别为
,两个焦点分别为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)过![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 两点,若
两点,若![]() 的内切圆半径为
的内切圆半径为![]() ,求以
,求以![]() 为圆心且与直线
为圆心且与直线![]() 相切的圆的方程.
相切的圆的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某水果批发商经销某种水果(以下简称![]() 水果),购入价为300元/袋,并以360元/袋的价格售出,若前8小时内所购进的
水果),购入价为300元/袋,并以360元/袋的价格售出,若前8小时内所购进的![]() 水果没有售完,则批发商将没售完的
水果没有售完,则批发商将没售完的![]() 水果以220元/袋的价格低价处理完毕(根据经验,2小时内完全能够把
水果以220元/袋的价格低价处理完毕(根据经验,2小时内完全能够把![]() 水果低价处理完,且当天不再购入).该水果批发商根据往年的销量,统计了100天
水果低价处理完,且当天不再购入).该水果批发商根据往年的销量,统计了100天![]() 水果在每天的前8小时内的销售量,制成如下频数分布条形图.
水果在每天的前8小时内的销售量,制成如下频数分布条形图.
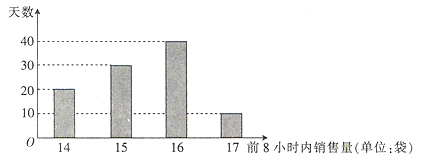
记![]() 表示
表示![]() 水果一天前8小时内的销售量,
水果一天前8小时内的销售量,![]() 表示水果批发商一天经营
表示水果批发商一天经营![]() 水果的利润,
水果的利润,![]() 表示水果批发商一天批发
表示水果批发商一天批发![]() 水果的袋数.
水果的袋数.
(1)若![]() ,求
,求![]() 与
与![]() 的函数解析式;
的函数解析式;
(2)假设这100天中水果批发商每天购入![]() 水果15袋或者16袋,分别计算该水果批发商这100天经营
水果15袋或者16袋,分别计算该水果批发商这100天经营![]() 水果的利润的平均数,以此作为决策依据,每天应购入
水果的利润的平均数,以此作为决策依据,每天应购入![]() 水果15袋还是16袋?
水果15袋还是16袋?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,直线
,直线![]() 过右焦点
过右焦点![]() ,过点
,过点![]() 的直线
的直线![]() 交椭圆
交椭圆![]() 于
于![]() ,
,![]() 两点(均不为顶点)
两点(均不为顶点)
(1)求椭圆![]() 的方程;
的方程;
(2)已知![]() 是椭圆
是椭圆![]() 的右顶点,直线
的右顶点,直线![]() ,若直线
,若直线![]() 与直线
与直线![]() 交于点
交于点![]() 直线
直线![]() 与直线
与直线![]() 交于点
交于点![]() ,试判断
,试判断![]() 是否为定值,若是,求出定值,若不是请说明理由.
是否为定值,若是,求出定值,若不是请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com