练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】在直角坐标系中，曲线，曲线（为参数），以坐标原点为极点，以轴的正半轴为极轴建立极坐标系.

    （1）求的极坐标方程；

    （2）射线的极坐标方程为，若分别与交于异于极点的两点，求的最大值.

    【答案】（1）的极坐标方程是，的极坐标方程是. （2）

    【解析】

    （1）利用将的直角坐标方程化为极坐标方程；先把的参数方程化为普通方程,再化为极坐标方程；

    （2）分别联立曲线与的极坐标方程与,即可求得,,再利用二次函数的性质求得的最大值,进而求解.

    解:（1）因为,

    所以可化为,

    整理得,

    （为参数）,则（为参数）,化为普通方程为,则极坐标方程为,即.

    所以的极坐标方程是,的极坐标方程是.

    （2）由（1）知,

    联立可得,

    联立可得,

    所以,

    当时,最大值为,所以的最大值为.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知函数，且x＝0是f（x）的极值点.

    （1）求f（x）的最小值；

    （2）是否存在实数b，使得关于x的不等式ex＜bx+f（x）在（0，+∞）上恒成立？若存在，求出b的取值范围；若不存在，说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】七巧板是中国古代劳动人民的发明，其历史至少可以追溯到公元前一世纪，后清陆以湉《冷庐杂识》卷一中写道“近又有七巧图，其式五，其数七，其变化之式多至千余”在18世纪，七巧板流传到了国外，被誉为“东方魔板”，至今英国剑桥大学的图书馆里还珍藏着一部《七巧新谱》．完整图案为一正方形(如图)：五块等腰直角三角形、一块正方形和一块平行四边形，如果在此正方形中随机取一点，那么此点取自阴影部分的概率是（ ）

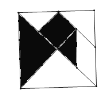
    A.B.C.D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆：过点，、分别为椭圆C的左、右焦点且

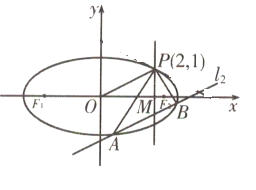
    （1）求椭圆C的方程；

    （2）直线平行于OP（O为原点），且与椭圆C交于两点A、B，与直线x＝2交于点M（M介于A、B两点之间）．

    （I）当△PAB面积最大时，求的方程；

    （II）求证：.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某科研团队对例新冠肺炎确诊患者的临床特征进行了回顾性分析.其中名吸烟患者中，重症人数为人，重症比例约为；名非吸烟患者中，重症人数为人，重症比例为.根据以上数据绘制列联表，如下：

    吸烟人数

    非吸烟人数

    总计

    重症人数

    30

    120

    150

    轻症人数

    100

    800

    900

    总计

    130

    920

    1050

    (1)根据列联表数据，能否在犯错误的概率不超过的前提下认为新冠肺炎重症和吸烟有关？

    (2)已知每例重症患者平均治疗费用约为万元，每例轻症患者平均治疗费用约为万元.现有吸烟确诊患者20人，记这名患者的治疗费用总和为，求.

    附：

    ≥

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】过轴正半轴上一点做直线与抛物线交于，，两点，且满足，过定点与点做直线与抛物线交于另一点，过点与点做直线与抛物线交于另一点.设三角形的面积为，三角形的面积为.

    （1）求正实数的取值范围；

    （2）连接，两点，设直线的斜率为；

    （ⅰ）当时，直线在轴的纵截距范围为，则求的取值范围；

    （ⅱ）当实数在（1）取到的范围内取值时，求的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在公比大于0的等比数列{an}中，已知a3a5＝a4，且a2，3a4，a3成等差数列．

    （1）求{an}的通项公式；

    （2）已知Sn＝a1a2…an，试问当n为何值时，Sn取得最大值，并求Sn的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知口袋里装有4个大小相同的小球，其中两个标有数字1，两个标有数字2．

    （1）从口袋里任意取一球，求取到标有数字2的球的概率；

    （2）第一次从口袋里任意取一球，放回口袋里后第二次再任意取一球，记第一次与第二次取到小球上的数字之和为．当为何值时，其发生的概率最大？说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知点，点A是直线上的动点，过作直线，，线段的垂直平分线与交于点.

    （1）求点的轨迹的方程；

    （2）若点，是直线上两个不同的点，且的内切圆方程为，直线的斜率为，求的取值范围.

    查看答案和解析>>

    同步练习册答案