
【题目】在公比大于0的等比数列{an}中,已知a3a5=a4,且a2,3a4,a3成等差数列.
(1)求{an}的通项公式;
(2)已知Sn=a1a2…an,试问当n为何值时,Sn取得最大值,并求Sn的最大值.
【答案】(1)an=24﹣n,n∈N*;(2)当n=3或4时,Sn取得最大值64.
【解析】
(1)设{an}的公比为q,(q>0),运用等比数列的通项公式和等差数列的中项性质,解方程可得首项和公比,即可得到所求通项公式;
(2)由等比数列的通项公式和等差数列的求和公式,可得Sn,结合二次函数的最值求法,可得所求最大值和n的值.
(1)设{an}的公比为![]() ,
,
由a3a5=a42=a4,可得a4=1,即a1q3=1,
因为a2,3a4,a3成等差数列,所以a2+a3=6a4,即a1q+a1q2=6a1q3,即6q2﹣q﹣1=0,
解得![]() 或
或![]() (舍去),所以a1=8,
(舍去),所以a1=8,
所以![]() .
.
(2)由(1)知![]() ,
,
所以![]() ,
,
又由![]() ,
,
所以当![]() 或
或![]() 时,
时,![]() 取得最大值,最大值为
取得最大值,最大值为![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
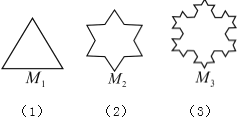
【题目】分形几何是一门以不规则几何形态为研究对象的几何学,科赫曲线是比较典型的分形图形,1904年瑞典数学家科赫第一次描述了这种曲线,因此将这种曲线称为科赫曲线.其生成方法是:(I)将正三角形(图(1))的每边三等分,以每边三等分后的中间的那一条线段为一边,向形外作等边三角形,并将这“中间一段”去掉,得到图(2);(II)将图(2)的每边三等分,重复上述的作图方法,得到图(3);(Ⅲ)再按上述方法继续做下去……,设图(1)中的等边三角形的边长为1,并且分别将图(1)、图(2)、图(3)、…、图(n)、…中的图形依次记作![]() ,
,![]() ,
,![]() ,…,
,…,![]() ,…,设
,…,设![]() 的周长为
的周长为![]() ,则
,则![]() 为( )
为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四面体ABCD中,△ABC和△BCD均是边长为1的等边三角形,已知四面体ABCD的四个顶点都在同一球面上,且AD是该球的直径,则四面体ABCD的体积为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() ,曲线
,曲线![]() (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,以
为极点,以![]() 轴的正半轴为极轴建立极坐标系.
轴的正半轴为极轴建立极坐标系.
(1)求![]() 的极坐标方程;
的极坐标方程;
(2)射线![]() 的极坐标方程为
的极坐标方程为![]() ,若
,若![]() 分别与
分别与![]() 交于异于极点的
交于异于极点的![]() 两点,求
两点,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某水果批发商经销某种水果(以下简称![]() 水果),购入价为300元/袋,并以360元/袋的价格售出,若前8小时内所购进的
水果),购入价为300元/袋,并以360元/袋的价格售出,若前8小时内所购进的![]() 水果没有售完,则批发商将没售完的
水果没有售完,则批发商将没售完的![]() 水果以220元/袋的价格低价处理完毕(根据经验,2小时内完全能够把
水果以220元/袋的价格低价处理完毕(根据经验,2小时内完全能够把![]() 水果低价处理完,且当天不再购入).该水果批发商根据往年的销量,统计了100天
水果低价处理完,且当天不再购入).该水果批发商根据往年的销量,统计了100天![]() 水果在每天的前8小时内的销售量,制成如下频数分布条形图.
水果在每天的前8小时内的销售量,制成如下频数分布条形图.
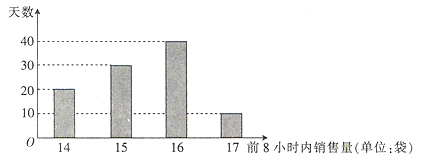
记![]() 表示
表示![]() 水果一天前8小时内的销售量,
水果一天前8小时内的销售量,![]() 表示水果批发商一天经营
表示水果批发商一天经营![]() 水果的利润,
水果的利润,![]() 表示水果批发商一天批发
表示水果批发商一天批发![]() 水果的袋数.
水果的袋数.
(1)若![]() ,求
,求![]() 与
与![]() 的函数解析式;
的函数解析式;
(2)假设这100天中水果批发商每天购入![]() 水果15袋或者16袋,分别计算该水果批发商这100天经营
水果15袋或者16袋,分别计算该水果批发商这100天经营![]() 水果的利润的平均数,以此作为决策依据,每天应购入
水果的利润的平均数,以此作为决策依据,每天应购入![]() 水果15袋还是16袋?
水果15袋还是16袋?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年春节前后,中国爆发新型冠状病毒(SARS-Cov-2)如图所示为1月24日至2月16日中国内地(除湖北以外的)感染新型冠状病毒新增人数的折线图,为了预测分析数据的变化规律,建立了![]() 与时间变量
与时间变量![]() 的不同时间段的两个线性回归模型.根据1月24日至2月3日的数据(时间变量
的不同时间段的两个线性回归模型.根据1月24日至2月3日的数据(时间变量![]() 的值依次为1,2,3,4,5,6,7,8,9,10,11)建立模型①:
的值依次为1,2,3,4,5,6,7,8,9,10,11)建立模型①:![]() ;根据2月4日至2月16日的数据(时间变量
;根据2月4日至2月16日的数据(时间变量![]() 的值依次为12,13,14,15,16,17,18,19,20,21,22,23,24)建立模型②:
的值依次为12,13,14,15,16,17,18,19,20,21,22,23,24)建立模型②:![]() .
.
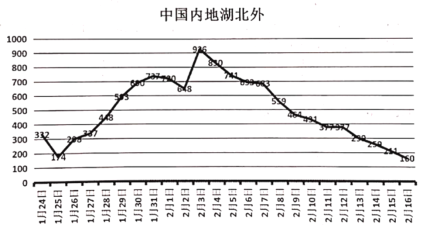
1月 24日 | 1月 25日 | 1月 26日 | 1月 27日 | 1月 28日 | 1月 29日 | 1月 30日 | 1月 31日 | 2月 1日 | 2月 2日 | 2月 3日 |
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
332 | 174 | 298 | 337 | 448 | 593 | 690 | 737 | 720 | 648 | 926 |
2月 4日 | 2月 5日 | 2月 6日 | 2月 7日 | 2月 8日 | 2月 9日 | 2月 10日 | 2月 11日 | 2月 12日 | 2月 13日 | 2月 14日 | 2月 15日 | 2月 16日 |
12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 |
830 | 741 | 693 | 683 | 559 | 464 | 431 | 377 | 377 | 299 | 259 | 211 | 160 |
(1)求出两个回归直线方程;(计算结果取整数)
(2)中国政府为了人民的生命安全,听取专家意见,了解了病毒信息,并迅速做出一系列的隔离防护措施,但新冠状病毒在世界范围内爆发时,某些欧美国家采取放任的态度,不治疗、不隔离、不检测,甚至不公布,请你用以上数据说明采取一系列措施的必要性,不采取措施的后果.
参考数据:![]() ,
,![]() ,
,![]() ,
,![]()
参考公式: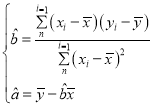 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com