
| A. | $\frac{π}{3}$ | B. | $\frac{π}{6}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{6}$ |
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
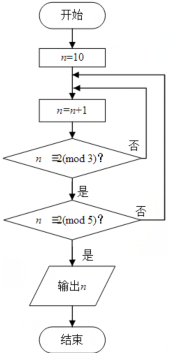 若正整数N除以正整数m后的余数为n,则记为N=n( mod m),例如10=2(mod 4).如图程序框图的算法源于我国古代闻名中外的《中国剩余定理》.执行该程序框图,则输出的n等于( )
若正整数N除以正整数m后的余数为n,则记为N=n( mod m),例如10=2(mod 4).如图程序框图的算法源于我国古代闻名中外的《中国剩余定理》.执行该程序框图,则输出的n等于( )| A. | 20 | B. | 21 | C. | 22 | D. | 23 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 我校教育处连续30天对同学们的着装进行检查,着装不合格的人数为如图所示的茎叶图,则中位数,众数,极差分别是( )
我校教育处连续30天对同学们的着装进行检查,着装不合格的人数为如图所示的茎叶图,则中位数,众数,极差分别是( )| A. | 44,45,56 | B. | 44,43,57 | C. | 44,43,56 | D. | 45,43,57 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
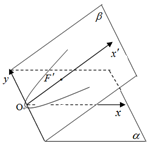 具有公共y轴的两个直角坐标平面α和β所成的二面角α-y轴-β等于60°,已知β内的曲线C'的方程是y2=4x',曲线C'在α内的射影在平面α内的曲线方程为y2=2px,则p=1.
具有公共y轴的两个直角坐标平面α和β所成的二面角α-y轴-β等于60°,已知β内的曲线C'的方程是y2=4x',曲线C'在α内的射影在平面α内的曲线方程为y2=2px,则p=1.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 56 | B. | 68 | C. | 78 | D. | 82 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,$\frac{1}{4}$] | B. | [0,$\frac{3}{8}$] | C. | ($\frac{1}{4}$,$\frac{1}{2}$] | D. | ($\frac{1}{4}$,$\frac{1}{2}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com