练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    如图1­5所示，在平面四边形ABCD中，AD＝1，CD＝2，AC＝.

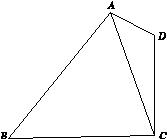
    图1­5

    (1)求cos∠CAD的值；

    (2)若cos∠BAD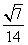＝－，sin∠CBA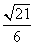＝，求BC的长．


    解：(1)在△ADC中，由余弦定理，得

    cos∠CAD＝，

    故由题设知，cos∠CAD＝＝.

    (2)设∠BAC＝α，则α＝∠BAD－∠CAD.

    因为cos∠CAD＝，cos∠BAD＝－，

    3.


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    已知集合A={z||z－2|≤2,z∈C},集合B={w|w=zi+b,b∈R},当A∩B=B时，求b的值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设函数f(x)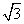＝sin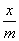，若存在f(x)的极值点x0满足x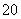＋[f(x0)]2＜m2，则m的取值范围是(　　)

    A．(－∞，－6)∪(6，＋∞)

    B．(－∞，－4)∪(4，＋∞)

    C．(－∞，－2)∪(2，＋∞)

    D．(－∞，－1)∪(1，＋∞)

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知△ABC的内角A，B，C满足sin 2A＋sin(A－B＋C)＝sin(C－A－B)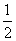＋，面积S满足1≤S≤2，记a，b，c分别为A，B，C所对的边，则下列不等式一定成立的是(　　)

    A．bc(b＋c)>8  B．ab(a＋b)>16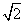 

    C．6≤abc≤12  D．12≤abc≤24

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    在△ABC中，内角A，B，C所对的边分别是a，b，c.已知b－c＝a，2sin B＝3sin C，则cos A的值为________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    △ABC的内角A，B，C所对的边分别为a，b，c.

    (1)若a，b，c成等差数列，证明：sin A＋sin C＝2sin(A＋C)；

    (2)若a，b，c成等比数列，求cos B的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


     已知函数f(x)＝(cos x－x)(π＋2x)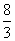－(sin x＋1)，g(x)＝3(x－π)cos x－4(1＋sin x)ln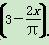.证明：

    (1)存在唯一x0∈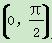，使f(x0)＝0；

    (2)存在唯一x1∈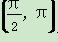，使g(x1)＝0，且对(1)中的x0，有x0＋x1<π.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


     已知函数f(x)＝x2＋2ax＋3，x∈[－1，1]，函数的最大值为

    求函数的表达式

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知函数.

    (1)若对于，恒成立，求实数的取值范围；

    (2)若对于，恒成立，求实数的取值范围

    查看答案和解析>>

    同步练习册答案