
分析 (1)由已知条件分别令n=1和n=2,能依次求出a2,a3.
(2)由已知得$\frac{{a}_{n+1}-1}{{2}^{n+1}}-\frac{{a}_{n}-1}{{2}^{n}}$=1,由此能求出实数λ使{$\frac{{a}_{n}+λ}{{2}^{n}}$}为等差数列,并利用错位相减法能求出由此求出an与Sn.
(3)由$\frac{S_n}{a_n}=\frac{{(n-1)•{2^{n+1}}+n+2}}{{n•{2^n}+1}}=2+\frac{{n-{2^{n+1}}}}{{n•{2^n}+1}}$,能求出n的所有取值,使$\frac{{S}_{n}}{{a}_{n}}$∈N*,
解答 解:(1)∵数列{an}的前n项和为Sn,a1=3,an+1=2an+2n+1-1(n∈N*),
∴${a}_{2}=2×3+{2}^{2}-1$=9,
${a}_{3}=2×9+{2}^{3}-1$=25.…(2分)
(2)∵a1=3,an+1=2an+2n+1-1(n∈N*),
∴an+1-1=2(an-1)+2n+1,
∴$\frac{{a}_{n+1}-1}{{2}^{n+1}}-\frac{{a}_{n}-1}{{2}^{n}}$=1,…(4分)
故λ=-1时,{$\frac{{a}_{n}+λ}{{2}^{n}}$}成等差数列,且首项为$\frac{{{a_1}-1}}{2}=1$,公差为d=1.
(注:由前3项列方程求出λ=-1后,没有证明的扣1分)
∴$\frac{{{a_n}-1}}{2^n}=n$即${a_n}=n•{2^n}+1$.…(5分)
此时${S_n}=(1×2+2×{2^2}+3×{2^3}+…+n×{2^n})+n$
令Tn=1×2+2×22+3×23+…+n×2n,则Sn=Tn+n,
又${T_n}=1×2+2×{2^2}+3×{2^3}+…+n×{2^n}$…①
则$2{T_n}=,1×{2^2}+2×{2^3}+3×{2^4}+…+n×{2^{n+1}}$…②
①-②得-Tn=2+22+23+…+2n-n×2n+1=(1-n)×2n+1-2,
∴Tn=(n-1)×2n+1+2,
∴${S_n}={T_n}+n=(n-1)×{2^{n+1}}+2+n$.…(8分)
(3)$\frac{S_n}{a_n}=\frac{{(n-1)•{2^{n+1}}+n+2}}{{n•{2^n}+1}}=2+\frac{{n-{2^{n+1}}}}{{n•{2^n}+1}}$…(9分)
结合y=2x及$y=\frac{1}{2}x$的图象可知${2^n}>\frac{n}{2}$恒成立,
∴2n+1>n,即n-2n+1<0,∵n•2n+1>0,∴$\frac{S_n}{a_n}<2$,…(10分)
当n=1时,$\frac{S_n}{a_n}=\frac{S_1}{a_1}=1∈{N_+}$…(11分)
当n≥2时,∵an>0且{an}为递增数列,∴Sn>0且Sn>an
∴$\frac{S_n}{a_n}>1$,即$1<\frac{S_n}{a_n}<2$,∴当n≥2时,$\frac{S_n}{a_n}∉{N_+}$,
综上可得n=1.…(12分)
点评 本题考查数列的通项公式和前n项和的求法,考查实数n的所有取值的求法,是中档题,解题时要认真审题,注意构造法和错位相减法的合理运用.


科目:高中数学 来源: 题型:选择题
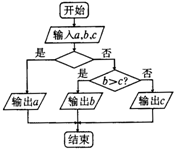
| A. | a>b? | B. | a>c? | C. | d>b或a>c? | D. | a>b且a>c? |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,$\frac{π}{3}$] | B. | [$\frac{π}{3}$,$\frac{π}{2}$) | C. | [$\frac{π}{6}$,$\frac{π}{3}$] | D. | ($\frac{π}{4}$,$\frac{π}{3}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
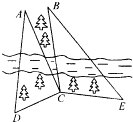 如图,为了开发某森林区,某测量人员身处这个森林区一条河的南岸,为了测量河对岸不能到达的两点A,B之间的距离,同时由于树木的遮挡,不可能分别在两个不同地点同时观察到点A,B;但她在南岸找到一个点C,从C点可以观察到点A,B;找到一个点D,从D点可以观察到点A,C;找到一个点E,从E点可以观察到点B,C;已知A,B,C,D,E在同一水平面内并测量得到数据:∠ACD=90°,∠ADC=60°,∠ACB=15°,∠BCE=105°,∠CEB=45°,DC=CE=1(km).
如图,为了开发某森林区,某测量人员身处这个森林区一条河的南岸,为了测量河对岸不能到达的两点A,B之间的距离,同时由于树木的遮挡,不可能分别在两个不同地点同时观察到点A,B;但她在南岸找到一个点C,从C点可以观察到点A,B;找到一个点D,从D点可以观察到点A,C;找到一个点E,从E点可以观察到点B,C;已知A,B,C,D,E在同一水平面内并测量得到数据:∠ACD=90°,∠ADC=60°,∠ACB=15°,∠BCE=105°,∠CEB=45°,DC=CE=1(km).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
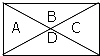 用5种不同的颜色给如图标有A,B,C,D的各部分涂色,每部分只涂一种颜色,且相邻两部分不同颜色,则不同的涂色方法共有( )
用5种不同的颜色给如图标有A,B,C,D的各部分涂色,每部分只涂一种颜色,且相邻两部分不同颜色,则不同的涂色方法共有( )| A. | 160种 | B. | 240种 | C. | 260种 | D. | 360种 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com