
如图,在四棱锥P-ABCD中,∠ABC=∠ACD=90°,∠BAC=∠CAD=60°,PA⊥平面ABCD,E为PD的中点,PA=2AB=2。

(1)求证:CE∥平面PAB;
(2)求四面体PACE的体积.
(1)详见解析;(2)
【解析】
试题分析:(1)要证CE∥平面PAB,可以转换为证明 ,而要证明
,而要证明 又可转化为
又可转化为 与
与 (另外也可以转化为线线平行) ;(2)要求四面体PACE的体积,可转换顶点求以E为顶点PAC为底面的三棱锥的体积.
(另外也可以转化为线线平行) ;(2)要求四面体PACE的体积,可转换顶点求以E为顶点PAC为底面的三棱锥的体积.
试题解析:(1)法一:取AD得中点M,连接EM,CM.

则EM//PA 1分
因为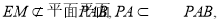
所以, 2分
2分
在 中,
中,
所以,
而 ,所以,MC//AB. 3分
,所以,MC//AB. 3分
因为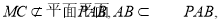
所以, 4分
4分
又因为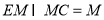
所以,
因为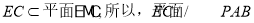 6分
6分
法二: 延长DC,AB,交于N点,连接PN. 1分
因为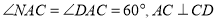
所以,C为ND的中点. 3分
因为E为PD的中点,所以,EC//PN
因为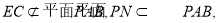
 6分
6分
(2)法一:由已知条件有;AC=2AB=2,AD=2AC=4,CD= 7分
7分
因为,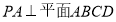 ,所以,
,所以, 8分
8分
又因为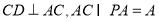
所以,  10分
10分
因为E是PD的中点
所以点E平面PAC的距离 ,
,
所以,四面体PACE的体积 12分
12分
法二:由已知条件有;AC=2AB=2,AD=2AC=4,CD=
因为,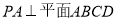
所以, 10分
10分
因为E是PD的中点
所以,四面体PACE的体积 12分
12分
考点:(1)空间位置关系的证明;(2)三棱锥求体积.


 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案 黄冈创优卷系列答案
黄冈创优卷系列答案科目:高中数学 来源:2014年高考数学三轮冲刺模拟 概率与统计(解析版) 题型:选择题
6位选手依次演讲,其中选手甲不在第一个也不在最后一个演讲,则不同的演讲次序共有( )
A.240种 B.360种 C.480种 D.720种
查看答案和解析>>
科目:高中数学 来源:2014年高考数学三轮冲刺模拟 三角函数、解三角形与平面向量(解析版) 题型:选择题
函数y= ln(1-x)的定义域为( )
ln(1-x)的定义域为( )
A.(0,1) B.[0,1) C.(0,1] D.[0,1]
查看答案和解析>>
科目:高中数学 来源:2014年吉林省延边州高考复习质量检测理科数学试卷(解析版) 题型:选择题
已知双曲线的一个焦点与抛物线 的焦点重合,且其渐近线的方程为
的焦点重合,且其渐近线的方程为 ,则该双曲线的标准方程为
,则该双曲线的标准方程为
A. B.
B. C.
C. D.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com