
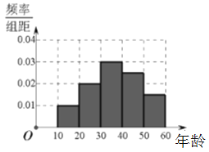
【题目】中国已经成为全球最大的电商市场,但是实体店仍然是消费者接触商品和品牌的重要渠道.某机构随机抽取了年龄介于10岁到60岁的消费者200人,对他们的主要购物方式进行问卷调查.现对调查对象的年龄分布及主要购物方式进行统计,得到如下图表:
主要购物方式 年龄阶段 | 网络平台购物 | 实体店购物 | 总计 |
40岁以下 | 75 | ||
40岁或40岁以上 | 55 | ||
总计 |
(1)根据已知条件完成上述列联表,并据此资料,能否在犯错误的概率不超过![]() 的前提下,认为消费者主要的购物方式与年龄有关?
的前提下,认为消费者主要的购物方式与年龄有关?
(2)用分层抽样的方法从通过网络平台购物的消费者中随机抽取8人,然后再从这8名消费者中抽取5名进行答谢.设抽到的消费者中40岁以下的人数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
参考公式: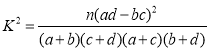 ,其中
,其中![]() .
.
临界值表:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
【答案】(1)可以在犯错误的概率不超过![]() 的前提下,认为消费者主要的购物方式与年龄有关;(2)见解析
的前提下,认为消费者主要的购物方式与年龄有关;(2)见解析
【解析】
(1)先由频率分布直方图得到列联表,再根据公式计算得到卡方值,进而作出判断;(2)消费者中40岁以下的人数为![]() ,可能取值为3,4,5,求出相应的概率值,再得到分布列和期望.
,可能取值为3,4,5,求出相应的概率值,再得到分布列和期望.
(1)根据直方图可知40岁以下的消费者共有![]() 人,40或40岁以上的消费者有80人,故根据数据完成列联表如下:
人,40或40岁以上的消费者有80人,故根据数据完成列联表如下:
年龄阶段 | 网络平台购物 | 实体店购物 | 总计 |
40岁以下 | 75 | 45 | 120 |
40岁或40岁以上 | 25 | 55 | 80 |
总计 | 100 | 100 | 200 |
依题意,![]() 的观测值
的观测值
![]()
![]()
故可以在犯错误的概率不超过![]() 的前提下,认为消费者主要的购物方式与年龄有关.
的前提下,认为消费者主要的购物方式与年龄有关.
(2)从通过网络平台购物的消费者中随机抽取8人,其中40岁以下的有6人,40岁或40岁以上的有2人,从这8名消费者抽取5名进行答谢,设抽到的消费者中40岁以下的人数为![]() ,则
,则![]() 的可能取值为3,4,5
的可能取值为3,4,5
且![]() ,
,
![]() ,
,
![]() ,
,
则![]() 的分布列为:
的分布列为:
| 3 | 4 | 5 |
|
|
|
|
![]()
故![]() 的数学期望为3.75.
的数学期望为3.75.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】某品牌计算机售后保修期为1年,根据大量的维修记录资料,这种品牌的计算机在使用一年内需要维修1次的占15%,需要维修2次的占6%,需要维修3次的占4%.
(1)某人购买了一台这个品牌的计算机,设![]() =“一年内需要维修k次”,k=0,1,2,3,请填写下表:
=“一年内需要维修k次”,k=0,1,2,3,请填写下表:
事件 |
|
|
|
|
概率 |
事件![]() 是否满足两两互斥?是否满足等可能性?
是否满足两两互斥?是否满足等可能性?
(2)求下列事件的概率:
①A=“在1年内需要维修”;
②B=“在1年内不需要维修”;
③C=“在1年内维修不超过1次”.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知平面内点![]() 到点
到点![]() 的距离和到直线
的距离和到直线![]() 的距离之比为
的距离之比为![]() ,若动点P的轨迹为曲线C.
,若动点P的轨迹为曲线C.
(I)求曲线C的方程;
(II)过F的直线![]() 与C交于A,B两点,点M的坐标为
与C交于A,B两点,点M的坐标为![]() 设O为坐标原点.证明:
设O为坐标原点.证明:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在长方体![]() 中,写出所有
中,写出所有
(1)与直线AB平行的直线,并用“∥”表示;
(2)与直线![]() 异面的直线;
异面的直线;
(3)与直线AB平行的平面,并用合适的符号表示;
(4)与平面![]() 平行的平面,并用合适的符号表示;
平行的平面,并用合适的符号表示;
(5)与直线AD垂直的平面,并用合适的符号表示.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某少儿游泳队需对队员进行限时的仰卧起坐达标测试.已知队员的测试分数![]() 与仰卧起坐
与仰卧起坐
个数![]() 之间的关系如下:
之间的关系如下: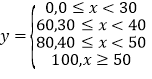 ;测试规则:每位队员最多进行三组测试,每组限时1分钟,当一组测完,测试成绩达到60分或以上时,就以此组测试成绩作为该队员的成绩,无需再进行后续的测试,最多进行三组;根据以往的训练统计,队员“喵儿”在一分钟内限时测试的频率分布直方图如下:
;测试规则:每位队员最多进行三组测试,每组限时1分钟,当一组测完,测试成绩达到60分或以上时,就以此组测试成绩作为该队员的成绩,无需再进行后续的测试,最多进行三组;根据以往的训练统计,队员“喵儿”在一分钟内限时测试的频率分布直方图如下:
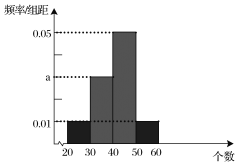
(1)计算![]() 值;
值;
(2)以此样本的频率作为概率,求
①在本次达标测试中,“喵儿”得分等于![]() 的概率;
的概率;
②“喵儿”在本次达标测试中可能得分的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知三棱锥![]() (如图1)的平面展开图(如图2)中,四边形
(如图1)的平面展开图(如图2)中,四边形![]() 为边长等于
为边长等于![]() 的正方形,
的正方形,![]() 和
和![]() 均为正三角形,在三棱锥
均为正三角形,在三棱锥![]() 中:
中:
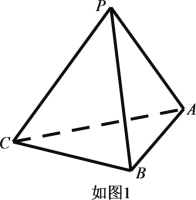

(1)证明:平面![]() 平面
平面![]() ;
;
(2)若点![]() 在棱
在棱![]() 上运动,当直线
上运动,当直线![]() 与平面
与平面![]() 所成的角最大时,求二面角
所成的角最大时,求二面角![]() 的正切值.
的正切值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某市举行的一次市质检考试中,为了调查考试试题的有效性以及试卷的区分度,该市教研室随机抽取了参加本次质检考试的500名学生的数学考试成绩,并将其统计如下表所示.

根据上表数据统计,可知考试成绩落在![]() 之间的频率为
之间的频率为![]() .
.
(Ⅰ)求m、n的值;
(Ⅱ)已知本欢质检中的数学测试成绩![]() ,其中
,其中![]() 近似为样本的平均数,
近似为样本的平均数,![]() 近似为样本方差
近似为样本方差![]() ,若该市有4万考生,试估计数学成绩介于
,若该市有4万考生,试估计数学成绩介于![]() 分的人数;
分的人数;![]() 以各组的区间的中点值代表该组的取值
以各组的区间的中点值代表该组的取值![]() Ⅲ
Ⅲ![]() 现按分层抽样的方法从成绩在
现按分层抽样的方法从成绩在![]() 以及
以及![]() 之间的学生中随机抽取12人,再从这12人中随机抽取4人进行试卷分析,记被抽取的4人中成绩在
之间的学生中随机抽取12人,再从这12人中随机抽取4人进行试卷分析,记被抽取的4人中成绩在![]() 之间的人数为X,求X的分布列以及期望
之间的人数为X,求X的分布列以及期望![]() .
.
参考数据:若![]() ,则
,则![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知过点![]() 的直线
的直线![]() 的参数方程是
的参数方程是 (
(![]() 为参数),以平面直角坐标系的原点为极点,
为参数),以平面直角坐标系的原点为极点,![]() 轴的正半轴为极轴,建立极坐标系,曲线
轴的正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,试问是否存在实数
两点,试问是否存在实数![]() ,使得
,使得![]() ?若存在,求出实数
?若存在,求出实数![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P﹣ABCD中,底面ABCD是一个菱形,三角形PAD是一个等腰三角形,∠BAD=∠PAD=![]() ,点E在线段PC上,且PE=3EC.
,点E在线段PC上,且PE=3EC.
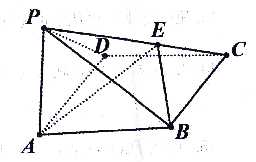
(1)求证:AD⊥PB;
(2)若平面PAD⊥平面ABCD,求二面角E﹣AB﹣P的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com