
分析 (1)由条件利用n次独立重复实验中恰好发生k次的概率,求得恰有3次击中目标的概率.
(2)求出他在4次射击中,全没有击中的概率,再用1减去此概率,即得所求.
解答 解:(1)他在4次射击中,恰有3次击中目标的概率为${C}_{4}^{3}$•${(\frac{1}{2})}^{3}$•$\frac{1}{2}$=$\frac{1}{4}$;
(2)他在4次射击中,全没有击中的概率为${(\frac{1}{4})}^{4}$=$\frac{1}{16}$,故他至少有1次击中目标的概率1-$\frac{1}{16}$=$\frac{15}{16}$.
点评 本题主要考查n次独立重复实验中恰好发生k次的概率,所求的事件的概率与它的对立事件的概率之间的关系,属于基础题.


 步步高达标卷系列答案
步步高达标卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,平面内有三个向量$\overrightarrow{OA},\;\overrightarrow{OB},\;\overrightarrow{OC}$,其中$\overrightarrow{OA}$与$\overrightarrow{OB}$的夹角为150°,$\overrightarrow{OA}$与$\overrightarrow{OC}$的夹角为90°,且$|{\overrightarrow{OA}}|=|{\overrightarrow{OB}}|=1$,$|{\overrightarrow{OC}}|=2$,若$\overrightarrow{OC}=λ\overrightarrow{OA}+μ\overrightarrow{OB}\;(λ,μ∈R)$,则λ+μ=( )
如图,平面内有三个向量$\overrightarrow{OA},\;\overrightarrow{OB},\;\overrightarrow{OC}$,其中$\overrightarrow{OA}$与$\overrightarrow{OB}$的夹角为150°,$\overrightarrow{OA}$与$\overrightarrow{OC}$的夹角为90°,且$|{\overrightarrow{OA}}|=|{\overrightarrow{OB}}|=1$,$|{\overrightarrow{OC}}|=2$,若$\overrightarrow{OC}=λ\overrightarrow{OA}+μ\overrightarrow{OB}\;(λ,μ∈R)$,则λ+μ=( )| A. | 2 | B. | 4 | C. | $\sqrt{3}$+2 | D. | 2$\sqrt{3}$+4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
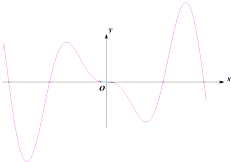
| A. | f(x)=xcosx-sinx | B. | f(x)=xsinx | C. | f(x)=xcosx+sinx | D. | f(x)=xcosx |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | -3 | C. | ±3 | D. | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 将一个长宽分别为2米和2k米(0<k<1)的铁皮的四角切去相同的正方形,然后折成一个无盖的长方体的盒子,记切去的正方形边长为x(0<x<k),
将一个长宽分别为2米和2k米(0<k<1)的铁皮的四角切去相同的正方形,然后折成一个无盖的长方体的盒子,记切去的正方形边长为x(0<x<k),查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a,b都小于等于1 | B. | a,b都大于1 | ||
| C. | a,b都大于等于1 | D. | a,b都小于1当a<0时 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com