
某同学用“五点法”画函数 在某一个周期内的图象时,列表并填入的部分数据如下表:
在某一个周期内的图象时,列表并填入的部分数据如下表:
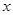 |  |  |  |  |  |
 |  |  |  |  |  |
 |  |  |  |  |  |
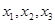 ,并直接写出函数
,并直接写出函数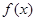 的解析式;
的解析式;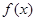 的图象沿
的图象沿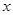 轴向右平移
轴向右平移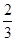 个单位得到函数
个单位得到函数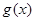 ,若函数
,若函数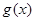 在
在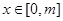 (其中
(其中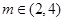 )上的值域为
)上的值域为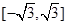 ,且此时其图象的最高点和最低点分别为
,且此时其图象的最高点和最低点分别为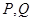 ,求
,求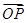 与
与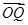 夹角
夹角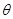 的大小。
的大小。 (1)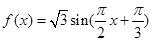 ;(2)
;(2)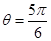 .
.
解析试题分析:本题主要考查五点作图法、三角函数图象的平移、三角函数值域、向量的夹角公式等基础知识,考查学生的分析问题解决问题的能力、计算能力,考查学生的数形结合思想.第一问,结合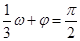 且
且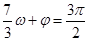 ,得出
,得出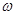 和
和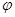 ,再解方程求出
,再解方程求出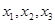 的值,再结合三角函数图象写出
的值,再结合三角函数图象写出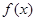 解析式;第二问,先将
解析式;第二问,先将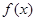 图象向右平移得到
图象向右平移得到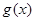 解析式,结合正弦图象,利用值域确定最高点、最低点的坐标,从而得到
解析式,结合正弦图象,利用值域确定最高点、最低点的坐标,从而得到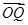 和
和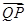 向量坐标,利用夹角公式求出
向量坐标,利用夹角公式求出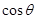 ,再确定角
,再确定角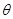 .
.
试题解析:(1)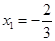 ,
,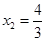 ,
,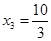 , 3分
, 3分
∴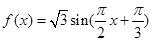 , 5分
, 5分
(2)将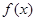 的图象沿x轴向右平移
的图象沿x轴向右平移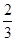 个单位得到函数
个单位得到函数 , 6分
, 6分
由于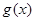 在
在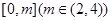 上的值域为
上的值域为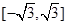 ,
,
则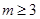 ,故最高点为
,故最高点为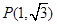 ,最近点为
,最近点为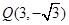 . 8分
. 8分
则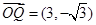 ,
,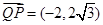 ,则
,则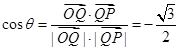 ,故
,故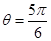 . 12分
. 12分
考点:五点作图法、三角函数图象的平移、三角函数值域、向量的夹角公式.


 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:高中数学 来源: 题型:解答题
如图,某市新体育公园的中心广场平面图如图所示,在y轴左侧的观光道曲线段是函数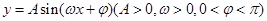 ,
,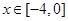 时的图象且最高点B(-1,4),在y轴右侧的曲线段是以CO为直径的半圆弧.⑴试确定A,
时的图象且最高点B(-1,4),在y轴右侧的曲线段是以CO为直径的半圆弧.⑴试确定A,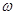 和
和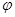 的值;⑵现要在右侧的半圆中修建一条步行道CDO(单位:米),在点C与半圆弧上的一点D之间设计为直线段(造价为2万元/米),从D到点O之间设计为沿半圆弧的弧形(造价为1万元/米).设
的值;⑵现要在右侧的半圆中修建一条步行道CDO(单位:米),在点C与半圆弧上的一点D之间设计为直线段(造价为2万元/米),从D到点O之间设计为沿半圆弧的弧形(造价为1万元/米).设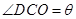 (弧度),试用
(弧度),试用 来表示修建步行道的造价预算,并求造价预算的最大值?(注:只考虑步行道的长度,不考虑步行道的宽度)
来表示修建步行道的造价预算,并求造价预算的最大值?(注:只考虑步行道的长度,不考虑步行道的宽度)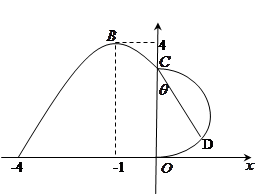
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com