
【题目】已知Sn为公差不为0的等差数列{an}的前n项和,且a1=1,S1 , S2 , S4成等比数列.
(1)求数列{an}的通项公式;
(2)设 ![]() ,求数列{bn}的前n项和.
,求数列{bn}的前n项和.
科目:高中数学 来源: 题型:
【题目】如图,水平放置的正四棱柱形玻璃容器Ⅰ和正四棱台形玻璃容器Ⅱ的高均为32cm,容器Ⅰ的底面对角线AC的长为10![]() cm,容器Ⅱ的两底面对角线EG,E1G1的长分别为14cm和62cm. 分别在容器Ⅰ和容器Ⅱ中注入水,水深均为12cm. 现有一根玻璃棒l,其长度为40cm.(容器厚度、玻璃棒粗细均忽略不计)
cm,容器Ⅱ的两底面对角线EG,E1G1的长分别为14cm和62cm. 分别在容器Ⅰ和容器Ⅱ中注入水,水深均为12cm. 现有一根玻璃棒l,其长度为40cm.(容器厚度、玻璃棒粗细均忽略不计)
(1)将l放在容器Ⅰ中,l的一端置于点A处,另一端置于侧棱CC1上,求l没入水中部分的长度;
(2)将l放在容器Ⅱ中,l的一端置于点E处,另一端置于侧棱GG1上,求l没入水中部分的长度.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两位打字员在两台电脑上各自输入![]() ,
, ![]() 两种类型的文件的部分文字才能使这两种类型的文件成为成品.已知
两种类型的文件的部分文字才能使这两种类型的文件成为成品.已知![]() 文件需要甲输入0.5小时,乙输入0.2小时;
文件需要甲输入0.5小时,乙输入0.2小时; ![]() 文件需要甲输入0.3小时,乙输入0.6小时.在一个工作日内,甲至多只能输入6小时,乙至多只能输入8小时,
文件需要甲输入0.3小时,乙输入0.6小时.在一个工作日内,甲至多只能输入6小时,乙至多只能输入8小时, ![]() 文件每份利润为60元,
文件每份利润为60元, ![]() 文件每份利润为80元,则甲、乙两位打字员在一个工作日内获得的最大利润是__________元.
文件每份利润为80元,则甲、乙两位打字员在一个工作日内获得的最大利润是__________元.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将一颗质地均匀的骰子先后抛掷2次,观察其向上的点数,分别记为x,y.
(1)若记“x+y=8”为事件A,求事件A发生的概率;
(2)若记“x2+y2≤12”为事件B,求事件B发生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,曲线
中,曲线![]() :
: ![]() (
(![]() 为参数,
为参数, ![]() ),在以坐标原点为极点,
),在以坐标原点为极点, ![]() 轴的非负半轴为极轴的极坐标系中,曲线
轴的非负半轴为极轴的极坐标系中,曲线![]() :
: ![]() .
.
(1)试将曲线![]() 与
与![]() 化为直角坐标系
化为直角坐标系![]() 中的普通方程,并指出两曲线有公共点时
中的普通方程,并指出两曲线有公共点时![]() 的取值范围;
的取值范围;
(2)当![]() 时,两曲线相交于
时,两曲线相交于![]() ,
, ![]() 两点,求
两点,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直四棱柱ABCD﹣A1B1C1D1中,A1C1⊥B1D1 , E,F分别是AB,BC的中点. 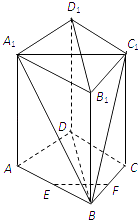
(1)求证:EF∥平面A1BC1;
(2)求证:平面D1DBB1⊥平面A1BC1 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知A(0,1)、B(0,2)、C(4t,2t2﹣1)(t∈R),⊙M是以AC为直径的圆,再以M为圆心、BM为半径作圆交x轴交于D、E两点.
(Ⅰ)若△CDE的面积为14,求此时⊙M的方程;
(Ⅱ)试问:是否存在一条平行于x轴的定直线与⊙M相切?若存在,求出此直线的方程;若不存在,请说明理由;
(Ⅲ)求 ![]() 的最大值,并求此时∠DBE的大小.
的最大值,并求此时∠DBE的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2016年高一新生入学后,为了了解新生学业水平,某区对新生进行了水平测试,随机抽取了50名新生的成绩,其相关数据统计如下:
分数段 | 频数 | 选择题得分24分以上(含24分) |
| 5 | 2 |
| 10 | 4 |
| 15 | 12 |
| 10 | 6 |
| 5 | 4 |
| 5 | 5 |
(Ⅰ)若从分数在![]() ,
, ![]() 的被调查的新生中各随机选取2人进行追踪调查,求恰好有2名新生选择题得分不足24分的概率;
的被调查的新生中各随机选取2人进行追踪调查,求恰好有2名新生选择题得分不足24分的概率;
(Ⅱ)在(Ⅰ)的条件下,记选中的4名新生中选择题得分不足24分的人数为![]() ,求随机变量
,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com