
分析 (1)f′(x)=a-x-$\frac{b}{x+1}$,(x>-1),g′(x)=ex-1.由曲线y=f(x)与y=g(x)在原点处有公共的切线,可得f′(0)=g′(0),b=a.因此f′(x)=$\frac{-x[x-(a-1)]}{x+1}$,对a分类讨论,利用导数研究函数的单调性即可得出.
(2)由g′(x)=ex-1,x>0时,g′(x)>0,可得ex≥x+1,从而x≥ln(x+1).设F(x)=g(x)-f(x)-$\frac{1}{2}$x2=ex+aln(x+1)-(a+1)x-1,F′(x)=ex+$\frac{a}{x+1}$-(a+1),对a分类讨论a=1,0<a<1,a>1,利用导数研究函数的单调性即可得出.
解答 解:(1)f′(x)=a-x-$\frac{b}{x+1}$,(x>-1),g′(x)=ex-1.
∵曲线y=f(x)与y=g(x)在原点处有公共的切线,
∴f′(0)=g′(0),∴a-b=0.∴b=a.
∴f′(x)=a-x-$\frac{a}{x+1}$=$\frac{-x[x-(a-1)]}{x+1}$,
a=1时,f′(x)=$\frac{-{x}^{2}}{x+1}$≤0,函数f(x)在(-1,+∞)上单调递减,舍去.
a>1时,x=0为f(x)的极小值点,舍去.
0<a<1时,-1<a-1<0,当x∈(-1,a-1)时,f′(x)<0,函数f(x)单调递减;x∈(a-1,0),f′(x)>0,函数f(x)单调递增;当x∈(0,+∞)时,
f′(x)<0,函数f(x)单调递减.∴x=0时,x=0为f(x)的极大值点.
因此可得:当x∈(-1,a-1)时,函数f(x)单调递减;x∈(a-1,0),函数f(x)单调递增;当x∈(0,+∞)时,函数f(x)单调递减.
(2)∵g′(x)=ex-1,x>0时,g′(x)>0,
故x=0时,g(x)取得最小值0,∴g(x)≥0,即ex≥x+1,从而x≥ln(x+1).
设F(x)=g(x)-f(x)-$\frac{1}{2}$x2=ex+aln(x+1)-(a+1)x-1,
F′(x)=ex+$\frac{a}{x+1}$-(a+1),
①a=1时,∵x≥0,∴F′(x)≥x+1+$\frac{a}{x+1}$-(a+1)=x+1+$\frac{1}{x+1}$-2≥0,
∴F(x)在[0,+∞)递增,从而F(x)≥F(0)=0,
即ex+ln(x+1)=2x-1>0,
∴g(x)≥f(x)+$\frac{1}{2}$x2.
②0<a<1时,由①得:ex+ln(x+1)-2x-1>0,
∴g(x)=ex-x-1≥x-ln(x+1)≥a(x-ln(x+1)),
故F(x)≥0即g(x)≥f(x)+$\frac{1}{2}$x2,
③a>1时,令h(x)=ex+$\frac{a}{x+1}$-(a+1),
则h′(x)=ex-$\frac{a}{{(x+1)}^{2}}$,
显然h′(x)在[0,+∞)递增,又h′(0)=1-a<0,h′($\sqrt{a}$-1)=${e}^{\sqrt{a}}$-1>0,
∴h′(x)在(0,$\sqrt{a}$-1)上存在唯一零点x0,
当x∈(0,x0)时,h′(x)<0,h(x)在[0,x0)递减,
x∈(0,x0)时,F(x)<F(0)=0,
即g(x)<f(x)+$\frac{1}{2}$x2,不合题意,
综上,a∈(0,1].
点评 本题考查了利用导数研究函数的单调性极值与最值,考查了等价转化能力、分类讨论方法、推理能力与计算能力,属于难题.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:高中数学 来源: 题型:解答题
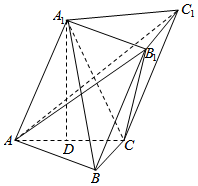 如图,三棱柱中ABC-A1B1C1中,点A1在平面ABC内的射影D为棱AC的中点,侧面A1ACC1为边长为2的菱形,AC⊥CB,BC=1.
如图,三棱柱中ABC-A1B1C1中,点A1在平面ABC内的射影D为棱AC的中点,侧面A1ACC1为边长为2的菱形,AC⊥CB,BC=1.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{4}{5}$ | B. | $\frac{3}{5}$ | C. | $\frac{3}{4}$ | D. | $\frac{4}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
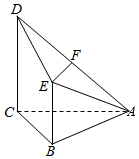 已知四棱锥A-BCDE,其中AB=BC=AC=BE=1,CD=2,CD⊥面ABC,BE∥CD,F为AD的中点.
已知四棱锥A-BCDE,其中AB=BC=AC=BE=1,CD=2,CD⊥面ABC,BE∥CD,F为AD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
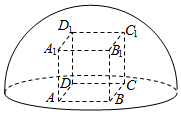 如图所示,直四棱柱ABCD-A1B1C1D1内接于半径为$\sqrt{3}$的半球O,四边形ABCD为正方形,则该四棱柱的体积最大时,AB的长是( )
如图所示,直四棱柱ABCD-A1B1C1D1内接于半径为$\sqrt{3}$的半球O,四边形ABCD为正方形,则该四棱柱的体积最大时,AB的长是( )| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com