
【题目】下列函数中,既是偶函数又在区间(0,+∞)上单调递减的是( )
A.![]()
B.y=e﹣x
C.y=lg|x|
D.y=﹣x2+1
【答案】D
【解析】解:A中,y= ![]() 为奇函数,故排除A;
为奇函数,故排除A;
B中,y=e﹣x为非奇非偶函数,故排除B;
C中,y=lg|x|为偶函数,在x∈(0,1)时,单调递减,在x∈(1,+∞)时,单调递增,
所以y=lg|x|在(0,+∞)上不单调,故排除C;
D中,y=﹣x2+1的图象关于y轴对称,故为偶函数,且在(0,+∞)上单调递减,
故选D.
【考点精析】本题主要考查了函数单调性的判断方法和函数的奇偶性的相关知识点,需要掌握单调性的判定法:①设x1,x2是所研究区间内任两个自变量,且x1<x2;②判定f(x1)与f(x2)的大小;③作差比较或作商比较;偶函数的图象关于y轴对称;奇函数的图象关于原点对称才能正确解答此题.


 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案科目:高中数学 来源: 题型:
【题目】某活动小组为了估计装有5个白球和若干个红球(每个球除颜色外都相同)的袋中红球接近多少个,在不将袋中球倒出来的情况下,分小组进行摸球试验,两人一组,共20组进行摸球实验.其中一位学生摸球,另一位学生记录所摸球的颜色,并将球放回袋中摇匀,每一组做400次试验,汇兑起来后,摸到红球次数为6000次.
(1)估计从袋中任意摸出一个球,恰好是红球的概率是 ;
(2)请你估计袋中红球接近 个.
查看答案和解析>>
科目:高中数学 来源: 题型:
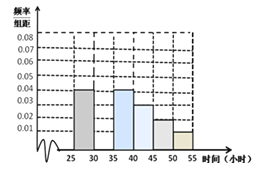
【题目】教育部,体育总局和共青团中央号召全国各级各类学校要广泛,深入地开展全国亿万大,中学生阳光体育运动,为此,某校学生会对高二年级2014年9月与10月这两个月内参加体育运动的情况进行统计,随机抽取了100名学生作为样本,得到这100名学生在该月参加体育运动总时间的小时数,根据此数据作出了如下的频数和频率的统计表和 频率分布直方图:
(I)求a,p的值,并补全频率分布直方图;
(Ⅱ)根据上述数据和直方图,试估计运动时间在[25,55]小时的学生体育运动的平均时间;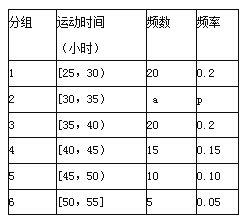
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】据报道,某公司的33名职工的月工资(以元为单位)如下:
职务 | 董事长 | 副董事长 | 董事 | 总经理 | 经理 | 管理员 | 职员 |
人数 | 1 | 1 | 2 | 1 | 5 | 3 | 20 |
工资 | 5 500 | 5 000 | 3 500 | 3 000 | 2 500 | 2 000 | 1 500 |
(1)求该公司职工月工资的平均数、中位数、众数;
(2)假设副董事长的工资从5000元提升到20000元,董事长的工资从5500元提升到30000元,那么新的平均数、中位数、众数又是什么?(精确到元)
(3)你认为哪个统计量更能反映这个公司员工的工资水平?结合此问题谈一谈你的看法.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ln(x+ ![]() ),
),
(1)判断并证明函数y=f(x)的奇偶性;
(2)判断并证明函数y=f(x)在R上的单调性;
(3)当x∈[1,2]时,不等式f(a4x)+f(2x+1)>0恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在极坐标系中,圆![]() 的极坐标方程为
的极坐标方程为![]() .若以极点
.若以极点![]() 为原点,极轴所在直线为
为原点,极轴所在直线为![]() 轴建立平面直角坐标系.
轴建立平面直角坐标系.
(Ⅰ)求圆![]() 的参数方程;
的参数方程;
(Ⅱ)在直角坐标系中,点![]() 是圆
是圆![]() 上动点,试求
上动点,试求![]() 的最大值,并求出此时点
的最大值,并求出此时点![]() 的直角坐标.
的直角坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知焦点在x正半轴上,顶点为坐标系原点的抛物线过点A(1,﹣2).
(1)求抛物线的标准方程;
(2)过抛物线的焦点F的直线l与抛物线交于两点M、N,且△MNO(O为原点)的面积为2 ![]() ,求直线l的方程.
,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】三棱锥P﹣ABC中,△ABC是底面,PA⊥PB,PA⊥PC,PB⊥PC,且这四个顶点都在半径为2的球面上,PA=2PB,则这个三棱锥的三个侧棱长的和的最大值为( )
A.16
B.![]()
C.![]()
D.32
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com