
分析 (Ⅰ)随机抽出的3篇课文中该学生能背诵的篇数为X,则X是一个随机变量,它的可能取值为0,1,2,3,分别求出相应的概率,由此能求出X的分布列.
( II)该学生能及格表示他能背出2或3篇,由此能求出他能及格的概率.
解答 解:(Ⅰ)随机抽出的3篇课文中该学生能背诵的篇数为X,则X是一个随机变量,它的可能取值为0,1,2,3,
且X服从超几何分布,
P(X=0)=$\frac{C_6^0C_4^3}{{C_{10}^3}}$=$\frac{1}{30}$.P(X=1)=$\frac{C_6^1C_4^2}{{C_{10}^3}}$=$\frac{3}{10}$,P(X=2)=$\frac{C_6^2C_4^1}{{C_{10}^3}}$=$\frac{1}{2}$,P(X=3)=$\frac{C_6^3C_4^0}{{C_{10}^3}}$=$\frac{1}{6}$,
∴X的分布列为:
| X | 0 | 1 | 2 | 3 |
| P | $\frac{1}{30}$ | $\frac{3}{10}$ | $\frac{1}{2}$ | $\frac{1}{6}$ |
点评 本题考查超几何分布模型,并能用该几何模型解决实际问题,是中档题,解题时要认真审题,注意排列组合知识的合理运用.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
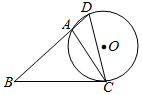 如图,在△ABC中,点D为线段BA延长线上的一点,且∠BDC=∠ACB,⊙O为△ADC的外接圆.
如图,在△ABC中,点D为线段BA延长线上的一点,且∠BDC=∠ACB,⊙O为△ADC的外接圆.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图所示,△ABC是直角三角形,∠ABC=90°,以AB为直径的圆O交AC于点E,点D是BC边的中点,连结OD交圆O于点M.且AB=4,DE=$\frac{3}{2}$.
如图所示,△ABC是直角三角形,∠ABC=90°,以AB为直径的圆O交AC于点E,点D是BC边的中点,连结OD交圆O于点M.且AB=4,DE=$\frac{3}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 几何题 | 代数题 | 总计 | |
| 男同学 | 30 | 8 | 30 |
| 女同学 | 8 | 12 | 20 |
| 总计 | 30 | 20 | 50 |
| P(k2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0,005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com