
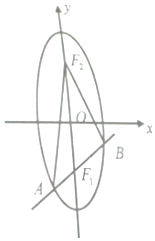
 已知椭圆的两个焦点F1、F2都在y轴上,且a=5,c=3.
已知椭圆的两个焦点F1、F2都在y轴上,且a=5,c=3.分析 (1)设出椭圆方程,利用条件求解即可.
(2)利用椭圆的定义,求解即可.
解答 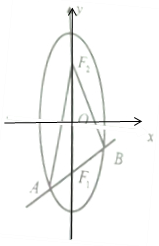 解:(1)因为椭圆焦点在y轴上,
解:(1)因为椭圆焦点在y轴上,
设所求椭圆的标准方程为:$\frac{y^2}{a^2}+\frac{x^2}{b^2}=1({a>b>0})$
因为a=5,c=3
所以b2=a2-c2=52-32=16,
所以所求椭圆的标准方程为:$\frac{y^2}{25}+\frac{x^2}{16}=1$
(2)由椭圆的定义有:|AF1|+|AF2|=2a,|BF1|+|BF2|=2a,△ABF2的周长为:|AB|+|AF2|+|BF2|=|AF1|+|BF1|+|AF2|+|BF2|=4a=20
点评 本题考查椭圆的方程的求法,椭圆的简单性质的应用,考查计算能力.


 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com