
分析 设AB=AC=2x,三角形的顶角θ,则由余弦定理求得cosθ的表达式,进而根据同角三角函数基本关系求得sinθ,最后根据三角形面积公式表示出三角形面积的表达式,根据一元二次函数的性质求得面积的最大值.
解答 解:在等腰△ABC中,设AB=AC=2x,AD=x.
设三角形的顶角为θ,则由余弦定理得cosθ=$\frac{5{x}^{2}-36}{4{x}^{2}}$,∴sinθ=$\frac{\sqrt{-9({x}^{2}-20)^{2}+6{0}^{2}-3{6}^{2}}}{4{x}^{2}}$,
由公式三角形:
S=$\frac{1}{2}$absinθ=$\frac{1}{2}•2x•2x•$$\frac{\sqrt{-9({x}^{2}-20)^{2}+6{0}^{2}-3{6}^{2}}}{4{x}^{2}}$=$\frac{1}{2}\sqrt{-9({x}^{2}-20)^{2}+6{0}^{2}-3{6}^{2}}$得:
当 x2=20时,三角形面积有最大值,即AB=2x=4$\sqrt{5}$时三角形面积有最大值.
所以答案为:4$\sqrt{5}$.
点评 本题考查了三角形的面积最值问题,设变量,用变量表达面积是关键,属于中档题.


 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案科目:高中数学 来源: 题型:选择题
| A. | (-1,1) | B. | (0,1) | C. | (-1,0) | D. | (-$\frac{2}{3}$,$\frac{2}{3}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
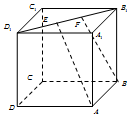 如图,正方体ABCD-A1B1C1D1的棱长为1,E,F是线段B1D上的两个动点,且EF=$\frac{\sqrt{2}}{2}$,则下列结论错误的是( )
如图,正方体ABCD-A1B1C1D1的棱长为1,E,F是线段B1D上的两个动点,且EF=$\frac{\sqrt{2}}{2}$,则下列结论错误的是( )| A. | AC⊥BF | B. | 直线AE、BF所成的角为定值 | ||
| C. | EF∥平面ABC | D. | 三棱锥A-BEF的体积为定值 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| X | 6 | 9 | 12 | 18 |
| P | a | $\frac{1}{3}$ | $\frac{1}{10}$ | $\frac{1}{15}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
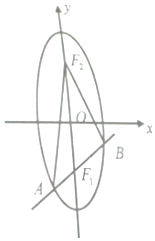 已知椭圆的两个焦点F1、F2都在y轴上,且a=5,c=3.
已知椭圆的两个焦点F1、F2都在y轴上,且a=5,c=3.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com