
【题目】已知函数![]()
![]() ,在一个周期内的图象如下图所示.
,在一个周期内的图象如下图所示.
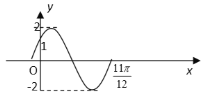
(1)求函数的解析式;
(2)设![]() ,且方程
,且方程![]() 有两个不同的实数根,求实数m的取值范围和这两个根的和.
有两个不同的实数根,求实数m的取值范围和这两个根的和.
科目:高中数学 来源: 题型:
【题目】某校学生会为了解高二年级600名学生课余时间参加中华传统文化活动的情况(每名学生最多参加7场).随机抽取50名学生进行调查,将数据分组整理后,列表如下:
参加场数 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
占调查人数的百分比 | 8% | 10% | 20% | 26% | 18% | m% | 4% | 2% |
则以下四个结论中正确的是( )
A.表中m的数值为10
B.估计该年级参加中华传统文化活动场数不高于2场的学生约为108人
C.估计该年级参加中华传统文化活动场数不低于4场的学生约为216人
D.若采用系统抽样方法进行调查,从该校高二600名学生中抽取容量为30的样本,则分段间隔为15
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某地三角工厂分别位于边长为2的正方形![]() 的两个顶点
的两个顶点![]() 及
及![]() 中点
中点![]() 处.为处理这三角工厂的污水,在该正方形区域内(含边界)与
处.为处理这三角工厂的污水,在该正方形区域内(含边界)与![]() 等距的点
等距的点![]() 处建一个污水处理厂,并铺设三条排污管道
处建一个污水处理厂,并铺设三条排污管道![]() ,记辅设管道总长为
,记辅设管道总长为![]() 千米.
千米.
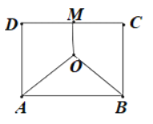
(1)按下列要求建立函数关系式:
(i)设![]() ,将
,将![]() 表示成
表示成![]() 的函数;
的函数;
(ii)设![]() ,将
,将![]() 表示成
表示成![]() 的函数;
的函数;
(2)请你选用一个函数关系,确定污水厂位置,使铺设管道总长最短.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 的前
的前![]() 项和为
项和为![]() ,
,![]() ,数列
,数列![]() 满足
满足![]() ,点
,点![]() 在直线
在直线![]() 上.
上.
(1)求数列![]() ,
,![]() 的通项公式
的通项公式![]() ,
,![]() ;
;
(2)令![]() ,求数列
,求数列![]() 的前
的前![]() 项和
项和![]() ;
;
(3)若![]() ,对所有的正整数
,对所有的正整数![]() 都有
都有![]() 成立,求
成立,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,不等式
,不等式![]() 对
对![]() 恒成立.
恒成立.
(1)求函数![]() 的极值和函数
的极值和函数![]() 的图象在点
的图象在点![]() 处的切线方程;
处的切线方程;
(2)求实数![]() 的取值的集合
的取值的集合![]() ;
;
(3)设![]() ,函数
,函数![]() ,
,![]() ,其中
,其中![]() 为自然对数的底数,若关于
为自然对数的底数,若关于![]() 的不等式
的不等式![]() 至少有一个解
至少有一个解![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
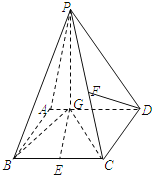
【题目】如图四棱锥![]() 中,底面ABCD是平行四边形,
中,底面ABCD是平行四边形,![]() 平面ABCD,垂足为G,G在AD上,且
平面ABCD,垂足为G,G在AD上,且![]() ,
,![]() ,
,![]() ,
,![]() ,E是BC的中点.
,E是BC的中点.
![]() 求异面直线GE与PC所成的角的余弦值;
求异面直线GE与PC所成的角的余弦值;
![]() 求点D到平面PBG的距离;
求点D到平面PBG的距离;
![]() 若F点是棱PC上一点,且
若F点是棱PC上一点,且![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将集合![]() 中的元素作全排列,使得除了最左端的一个数之外,对于其余的每个数
中的元素作全排列,使得除了最左端的一个数之外,对于其余的每个数![]() ,在
,在![]() 的左边某个位置上总有一个数与
的左边某个位置上总有一个数与![]() 之差的绝对值为1.则满足条件的排列个数为____________.
之差的绝对值为1.则满足条件的排列个数为____________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com