练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知以点P为圆心的圆经过点A(－1,0)和B(3,4)，线段AB的垂直平分线交圆P于点C和D，且|CD|＝4.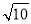

    (1)求直线CD的方程；

    (2)求圆P的方程．

     

    （1）x＋y－3＝0 （2）(x＋3)2＋(y－6)2＝40或(x－5)2＋(y＋2)2＝40

    【解析】(1)直线AB的斜率k＝1，AB的中点坐标为(1,2)，

    ∴直线CD的方程为y－2＝－(x－1)，即x＋y－3＝0.

    (2)设圆心P(a，b)，

    则由P在CD上得a＋b－3＝0.①

    又直径|CD|＝4，

    ∴|PA|＝2.

    ∴(a＋1)2＋b2＝40.②

    由①②解得或

    ∴圆心P(－3,6)或P(5，－2)．

    ∴圆P的方程为(x＋3)2＋(y－6)2＝40或(x－5)2＋(y＋2)2＝40.

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：2015高考数学（理）一轮配套特训：8-8曲线与方程（解析版） 题型：选择题

    长为3的线段AB的端点A、B分别在x轴、y轴上移动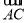，＝2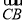，则点C的轨迹是(　　)

    A．线段 B．圆 C．椭圆 D．双曲线

     

    查看答案和解析>>

    科目：高中数学 来源：2015高考数学（理）一轮配套特训：8-5椭圆（解析版） 题型：填空题

    F1，F2是椭圆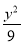＋＝1的左、右两焦点，P为椭圆的一个顶点，若△PF1F2是等边三角形，则a2＝________．

     

    查看答案和解析>>

    科目：高中数学 来源：2015高考数学（理）一轮配套特训：8-4直线与圆、圆与圆的位置关系（解析版） 题型：选择题

    已知圆C：x2＋(y－3)2＝4，过A(－1,0)的直线l与圆C相交于P，Q两点，若|PQ|＝2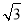，则直线l的方程为(　　)

    A．x＝－1或4x＋3y－4＝0

    B．x＝－1或4x－3y＋4＝0

    C．x＝1或4x－3y＋4＝0

    D．x＝1或4x＋3y－4＝0

     

    查看答案和解析>>

    科目：高中数学 来源：2015高考数学（理）一轮配套特训：8-3圆的方程（解析版） 题型：填空题

    已知圆C：(x－3)2＋(y－4)2＝1，点A(－1,0)，B(1,0)，点P为圆上的动点，则d＝|PA|2＋|PB|2的最大值为________，最小值为________．

     

    查看答案和解析>>

    科目：高中数学 来源：2015高考数学（理）一轮配套特训：8-3圆的方程（解析版） 题型：选择题

    过点M(1,2)的直线l将圆(x－2)2＋y2＝9分成两段弧，当其中的劣弧最短时，直线的方程是(　　)

    A．x＝1 B．y＝1

    C．x－y＋1＝0 D．x－2y＋3＝0

     

    查看答案和解析>>

    科目：高中数学 来源：2015高考数学（理）一轮配套特训：8-2直线的交点坐标与距离公式（解析版） 题型：选择题

    如图所示，已知A(4,0)，B(0,4)，从点P(2,0)射出的光线经直线AB反射后再射到直线OB上，最后经直线OB反射后又回到P点，则光线所经过的路程是(　　)

    A．2 B．6 C．3 D．2

     

    查看答案和解析>>

    科目：高中数学 来源：2015高考数学（理）一轮配套特训：8-1直线的倾斜角与斜率、直线方程（解析版） 题型：选择题

    设M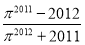＝，N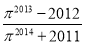＝，则M与N的大小关系为(　　)

    A．M>N B．M＝N C．M<N D．无法判断

     

    查看答案和解析>>

    科目：高中数学 来源：2015高考数学（理）一轮配套特训：7-5直线、平面垂直的判定及性质（解析版） 题型：解答题

    如图所示，在四棱锥P－ABCD中，四边形ABCD为菱形，△PAD为等边三角形，平面PAD⊥平面ABCD，且∠DAB＝60°，AB＝2，E为AD的中点．

    (1)求证：AD⊥PB；

    (2)求点E到平面PBC的距离．

     

    查看答案和解析>>

    同步练习册答案