
| A. | (0,$\frac{2}{3}$$\sqrt{3}$] | B. | (1,2] | C. | (1,0] | D. | [$\frac{1}{2}$,$\frac{2}{3}$$\sqrt{3}$] |
分析 设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$,如图所示:则$\overrightarrow{BC}$=$\overrightarrow{AC}-\overrightarrow{AB}$.由$\overrightarrow{a}$与$\overrightarrow{b}$-$\overrightarrow{a}$的夹角为120°,可得∠ABC=60°,再利用正弦定理即可得出.
解答 解:设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$,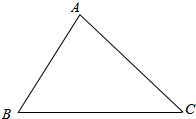
如图所示:
则$\overrightarrow{BC}$=$\overrightarrow{AC}-\overrightarrow{AB}$.
又∵$\overrightarrow{a}$与$\overrightarrow{b}$-$\overrightarrow{a}$的夹角为120°,
∴∠ABC=60°
又$|\overrightarrow{b}|$=$|\overrightarrow{AC}|$|=1
由正弦定理可得:$\frac{1}{sin6{0}^{°}}$=$\frac{|\overrightarrow{a}|}{sinC}$,
可得$|\overrightarrow{a}|$=$\frac{2\sqrt{3}}{3}$sinC≤$\frac{2\sqrt{3}}{3}$.
∴|$\overrightarrow{a}$|的取值范围是$(0,\frac{2\sqrt{3}}{3}]$.
故选:A.
点评 本题考查了向量的三角形法则、正弦定理、三角函数的单调性与值域,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
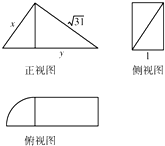
| A. | 2$\sqrt{15}$+$\frac{{\sqrt{15}π}}{12}$ | B. | 1+$\frac{π}{12}$ | C. | $\sqrt{15}$+$\frac{{\sqrt{15}π}}{4}$ | D. | 1+$\frac{{\sqrt{15}π}}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图所示,某射手射击小球,共打9枪,每枪都击中一个小球.球共有3串,他每次射击必须打某一串最下面的一个小球.其中,第5枪打中A,第6枪打中B的不同射击方法一共有12种.
如图所示,某射手射击小球,共打9枪,每枪都击中一个小球.球共有3串,他每次射击必须打某一串最下面的一个小球.其中,第5枪打中A,第6枪打中B的不同射击方法一共有12种.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
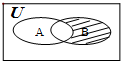 设全集U=Z,A={2,3,5,8,9},B={1,2,3,4,5,6},则图中阴影部分表示的集合是( )
设全集U=Z,A={2,3,5,8,9},B={1,2,3,4,5,6},则图中阴影部分表示的集合是( )| A. | {2,4,6} | B. | {1,3,5} | C. | {2,5,6} | D. | {1,4,6} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{3}{4}$ | D. | $\frac{4}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 2 | C. | -3 | D. | $\frac{1}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com