
| A. | 2$\sqrt{15}$+$\frac{{\sqrt{15}π}}{12}$ | B. | 1+$\frac{π}{12}$ | C. | $\sqrt{15}$+$\frac{{\sqrt{15}π}}{4}$ | D. | 1+$\frac{{\sqrt{15}π}}{4}$ |
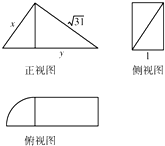
分析 由已知中的三视图,可知该几何体是一个三棱柱和一个四分之一的圆锥组合而成的几何体.该几何体的体积等于分别求的体积之和.设高为h,利用h把x,y的关系建立起来,在利用基本不等式就最值,确定h的值.
解答 解:由题中的三视图可知:该几何体是一个三棱柱和一个四分之一的圆锥组合而成的几何体.圆锥和棱柱的体积之和就是该几何体棱的体积.
设高为h,半径r=1,则有:1+h2=x2,h2+y2=31,消去h得:32=x2+y2≥2xy,那么:xy≤16.
当且仅当x=y=4时,xy取得最大值16.此时h=$\sqrt{15}$.
${V}_{圆锥}=\frac{1}{4}π{r}^{2}$h×$\frac{1}{3}$=$\frac{\sqrt{15}}{12}π$
$V柱=Sh=\frac{1}{2}×4×\sqrt{15}×1=2\sqrt{15}$
${V}_{总}=\frac{\sqrt{15}}{12}π+2\sqrt{15}$
故选:A
点评 本题考查了三视图的识图能力,能通过三视图准确知道该几何体的组成.利用三视图中的尺寸关系建立等式构造基本不等式是解题的关键.属于中档题.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:高中数学 来源: 题型:选择题
| A. | ( 0,1) | B. | ( 1,2) | C. | ( 2,4) | D. | (4,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,$\frac{2}{3}$$\sqrt{3}$] | B. | (1,2] | C. | (1,0] | D. | [$\frac{1}{2}$,$\frac{2}{3}$$\sqrt{3}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 年份 | 1896年 | 1900年 | 1904年 | … | 2016年 |
| 届数 | 1 | 2 | 3 | … | n |
| A. | 29 | B. | 30 | C. | 31 | D. | 32 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com