
分析 (1)设点P关于直线l的对称点P′(a,b),则$\left\{\begin{array}{l}{\frac{b-0}{a-2}×1=-1}\\{\frac{a+2}{2}-\frac{0+b}{2}-1=0}\end{array}\right.$,解得P′(1,1),求出直线P′Q的方程.则经过P′Q的直线与l相交于点M,即可对称.
(2)设M(x,x-1),利用两点之间的距离公式可得PM2+QM2=4$(x-\frac{1}{2})^{2}$+5,即可得出.
解答 解:如图所示,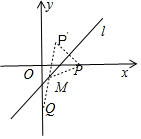
(1)设点P关于直线l的对称点P′(a,b),则$\left\{\begin{array}{l}{\frac{b-0}{a-2}×1=-1}\\{\frac{a+2}{2}-\frac{0+b}{2}-1=0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{a=1}\\{b=1}\end{array}\right.$,∴P′(1,1),
直线P′Q的方程为:y=$\frac{-2-1}{0-1}$x-2,即y=3x-2.
则经过P′Q的直线与l相交于点M,即为所求.
联立$\left\{\begin{array}{l}{y=3x-2}\\{x-y-1=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=\frac{1}{2}}\\{y=-\frac{1}{2}}\end{array}\right.$.M$(\frac{1}{2},-\frac{1}{2})$.
PM+QM的最小值=|P′Q|=$\sqrt{{1}^{2}+(1+2)^{2}}$=$\sqrt{10}$.
(2)设M(x,x-1),则PM2+QM2=(x-2)2+(x-1)2+x2+(x+1)2=4x2-4x+6=4$(x-\frac{1}{2})^{2}$+5,
∴当x=$\frac{1}{2}$,y=-$\frac{1}{2}$时,PM2+QM2的最小值为5.
点评 本题考查了对称性、相互垂直平分的性质、两点之间的距离公式、二次函数的单调性,考查了推理能力与计算能力,属于中档题.


 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
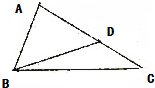 如图,在△ABC中,sin$\frac{∠ABC}{2}=\frac{{\sqrt{3}}}{3}$,AB=2,点D在线段AC上,且AD=2DC,BD=$\frac{{4\sqrt{3}}}{3}$,则cos∠ACB=$\frac{7}{9}$.
如图,在△ABC中,sin$\frac{∠ABC}{2}=\frac{{\sqrt{3}}}{3}$,AB=2,点D在线段AC上,且AD=2DC,BD=$\frac{{4\sqrt{3}}}{3}$,则cos∠ACB=$\frac{7}{9}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,3) | B. | (1,3) | C. | (0,2) | D. | (1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
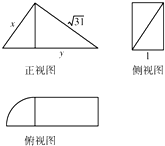
| A. | 2$\sqrt{15}$+$\frac{{\sqrt{15}π}}{12}$ | B. | 1+$\frac{π}{12}$ | C. | $\sqrt{15}$+$\frac{{\sqrt{15}π}}{4}$ | D. | 1+$\frac{{\sqrt{15}π}}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5,10,15 | B. | 3,9,18 | C. | 3,10,17 | D. | 5,9,16 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com