考点:棱柱、棱锥、棱台的体积,直线与平面平行的判定,直线与平面垂直的判定
专题:综合题,空间位置关系与距离
分析:(Ⅰ)根据线面垂直的判定定理,要证BD⊥面A
1ACC
1,只证BD⊥AC,BD⊥AA
1即可;
(Ⅱ)利用三角形的中位线的性质证明AC
1∥OP,即可证明AC
1∥平面PBD;
(Ⅲ)证明△A
1OP为等腰三角形,利用V
A1-BOP=
S
△A1OP•OB求三棱锥A
1-BOP的体积.
解答:
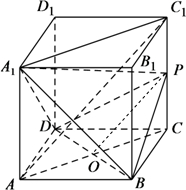
(Ⅰ)证明:在长方体AC
1中,∵底面ABCD是边长为4的正方形,∴对角线BD⊥AC.
又∵A
1A⊥平面ABCD,∴A
1A⊥BD.
AC∩A
1A=A,AC?面A
1ACC
1,A
1A?面A
1ACC
1;
∴BD⊥面A
1ACC
1.
(Ⅱ)证明:连接PO,则
∵点P是侧棱C
1C的中点,O是AC的中点,
∴AC
1∥OP,
∵AC
1?平面PBD,OP?平面PBD,
∴AC
1∥平面PBD;
(Ⅲ)解:∵AA
1=2
,AO=
,∴A
1O=
,
同样计算可得A
1P=
,∴△A
1OP为等腰三角形,
∵CO=CO=
,∴OP=2,
∴等腰三角形A
1OP的高为3,
∴V
A1-BOP=
S
△A1OP•OB=
.
点评:本题考查线面垂直的判定、线面垂直的性质及锥体的体积求解,考查学生综合运用知识解决问题的能力,属中档题.

 如图:已知长方体ABCD-A1B1C1D1的底面ABCD是边长为2的正方形,高AA1=2
如图:已知长方体ABCD-A1B1C1D1的底面ABCD是边长为2的正方形,高AA1=2 (Ⅰ)证明:在长方体AC1中,∵底面ABCD是边长为4的正方形,∴对角线BD⊥AC.
(Ⅰ)证明:在长方体AC1中,∵底面ABCD是边长为4的正方形,∴对角线BD⊥AC.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案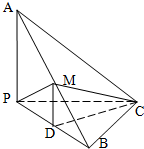 如图,已知三棱锥A-PBC中,AC⊥BC,AP⊥PC,M为AB的中点,D为PB的中点,且△PMB为正三角形.
如图,已知三棱锥A-PBC中,AC⊥BC,AP⊥PC,M为AB的中点,D为PB的中点,且△PMB为正三角形.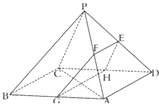 如图,四棱锥P-ABCD中,底面ABCD是边长为2
如图,四棱锥P-ABCD中,底面ABCD是边长为2 如图,三棱柱ABC-A1B1C1是直棱柱,AB⊥AC,AB=AC=AA1=2,点MN分别为A1B和B1C1的中点.
如图,三棱柱ABC-A1B1C1是直棱柱,AB⊥AC,AB=AC=AA1=2,点MN分别为A1B和B1C1的中点.